今天是 3 月 14 日。而圆周率 π 就约等于 3.14,因此这一天被设为了圆周率日。世界各地的数学家和数学爱好者们欢聚一堂,歌颂赞美这个数学世界中的奇迹。
大家或许会好奇,π 究竟哪点吸引人了,能够让数学家们对它痴迷到如此地步?其实,π 本身的存在就是一个奇迹:不管一个圆有多大,它的周长和直径之比总是一个固定的数,它就是 3.141592653589793 … ,是一个无限不循环小数。我们把这个数就叫做圆周率,用希腊字母 π 来表示。在几何问题中,圆周率扮演着非常重要的角色;然而更神奇的是,它也驰骋于几何以外的其它数学领域。
布丰投针实验

在地板上画一系列间距为 2 厘米的平行线,然后把一根长度为 1 厘米的针扔在地板上。那么,这根针与地板上的线条相交的概率是多少呢?1733 年,法国博物学家布丰(Comte de Buffon)第一次提出了这个问题。1777 年,布丰自己解决了这个问题——这个概率值是 1/π 。
这个问题可以用微积分直接求解,也能利用期望值的性质得到一个异常精妙的解答。即使我们现在已经能轻易求出它的答案,结论依然相当令人吃惊——在这个概率问题上,竟然也有 π 的踪影。有人甚至利用投针法,求出过 π 的近似值来。
斯特林近似公式
我们把从 1 开始一直连乘到 n 的结果称作“n 的阶乘”,在数学中用 n! 来表示。也就是说:
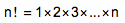
1733 年,数学家亚伯拉罕·棣莫弗(Abraham de Moivre)发现,当 n 很大的时候,有:
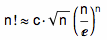
其中 c 是某个固定常数。不过棣莫弗本人并没有求出这个常数的准确值。几年后,数学家詹姆斯·斯特林(James Stirling)指出,这个常数 c 等于 2π 的平方根。也就是说:
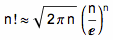
这个公式就被称作斯特林近似公式。
伽马函数
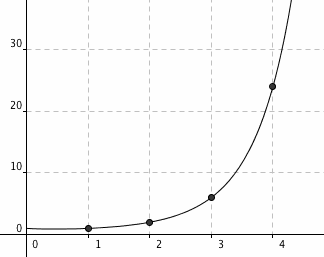
阶乘运算本来是定义在正整数上的,但我们可以很自然地把它扩展到所有的正数上——只需要寻找一条经过所有形如 (n, n!) 的整格点的曲线就可以了。由此定义出来的函数就叫做伽马函数,用希腊字母 Г 来表示。好了,神奇的事情出现了。我们有这样一个结论:
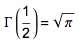
π 再次出现在了与几何毫无关系的场合中!
平方数的倒数和的极限
1 的平方分之一,加上 2 的平方分之一,加上 3 的平方分之一,这样一直加下去,结果会怎样呢?这是一个非常吸引人的问题。
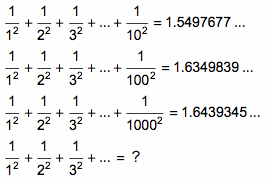
从上表中可以看到,越往后加,得数变化幅度就越小。可以预料,如果无穷地加下去,得数将会无限接近于某一个固定的数。这个数是多少呢?
1735 年,大数学家欧拉(Euler)非常漂亮地解决了这一问题。神奇的是,这个问题的答案里竟然包含有 π:
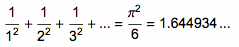
两个整数互质的概率
如果两个整数的最大公约数为 1,我们就说这两个数是互质的。例如,9 和 14 就是互质的,除了 1 以外它们没有其它的公共约数;9 和 15 就不互质,因为它们有公共的约数 3。可以证明这样一个令人吃惊的结论:任取两个整数,它们互质的概率是 6 / π 2 ,恰好是上面一个问题的答案的倒数。在一个纯数论领域的问题中出现了圆周率,无疑给小小的希腊字母 π 更添加了几分神秘。
欧拉恒等式
这是整个数学领域中最伟大,最神奇的公式:
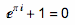
这个公式用加法、乘法、乘方这三个最基础的运算,把数学中最神奇的三个常数(圆周率 π、自然底数 e、虚数单位 i)以及最根本的两个数(0 和 1)联系在了一起,没有任何杂质,没有任何冗余,漂亮到了令人敬畏的地步。这个等式也是由大数学家欧拉发现的,它就是传说中的欧拉恒等式(Euler's identity)。《数学情报》杂志(The Mathematical Intelligencer)曾举办过一次读者投票活动,欧拉恒等式被评选为“史上最美的公式”。
然而,这些也都只是数学这个奇妙大世界的其中一角罢了。
