（文/Philip Ball）作为当今所有数字计算的基础，二进制算术通常被认为是18世纪初的戈特弗里德·莱布尼茨（Gottfried Leibniz）发明的。可现在有项研究称，早在此前300年，一个太平洋小岛，法属波利尼西亚的曼加雷瓦（Mangareva）上，人们已经在使用某种二进制系统了。
法属波利尼西亚的曼格雷哇的位置。 图片截自谷歌地图
曼格雷哇文化及语言，目前已经基本上被现代社会同化，发表在《美国国家科学院院刊》（Proceedings of the National Academy of Sciences）上的这项研究，通过对其史料的分析，表明，莱布尼茨提出的二进制系统的几个优点，即使在没有先进科技的社会，也许可以自发的产生。
纯粹的二进制算术以2为基数，而非常见的以10为基数。大概是因为人有十根手指，许多文化都选择了后者。以2做基数时，数以2的幂的形式表示出来：并非一、十、百（十的二次方）、千（十的三次方）等等，而是一（二的零次方）、二（二的一次方）、四（二的二次方）、八（二的三次方）等。
所有数都可以像这样仅用1和0表示出来，这样就能在计算机中编码成电脉冲或开关的接通与闭合状态。比如13表示成二进制就是1101（23 + 22+(0 × 21) + 20）。
莱布尼茨在1703年指出，用二进制做类似加与乘这种简单算术时，不必去记 5+4=9 或 6×7=42 这种规律。相反你只需应用一点简单的规律。拿加法来说，你只需要记住1加0得1，并且1+1得到进位的1就行了，比如100+101=1001。
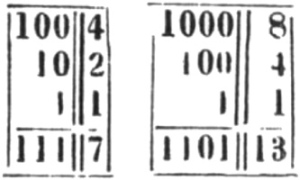莱布尼茨关于2进制的出版物，图片来自Nature News
混合系统
二进制的劣势在于，表示大数需要很多位。不过这项最新研究的作者，挪威卑尔根大学心理学家安德烈娅·本德尔（Andrea Bender）和西格哈德·贝勒（Sieghard Beller）认为，显然，曼加雷瓦人在1450年之前就找到了一个漂亮的解决办法。
以曼加雷瓦为主题的画作。图片来源：Nature News
曼加雷瓦是个火山岛，最初有人定居是在公元500到800年间。在18世纪跟欧洲人大量接触之前，其上可能有几千居民。高度分层的社会主要仰赖海产和块根作物，同时也需要一个记数系统，来计量在贸易与酋长上贡中产生的大交易额。
目前岛上大约只有六百名讲曼加雷瓦语的人，随着法国的殖民，其原有记数系统，早已无法挽回地被阿拉伯数字所取代。然而按照19世纪和20世纪早期（主要是欧洲的）作者们的描述，本德尔和贝勒重建了它。
他们发现曼加雷瓦先民将十进制和二进制结合了起来。先民们有表示数字1到10的单词，还有一些表示2的幂与10相乘的单词。“takau”这个词（本德尔和贝勒将其记为“K”）代表10；paua（P）代表20；tataua（T）代表40；varu（V）代表80。举个例子，用这些符号，70被表示成TPK，57被表示成TK7。
本德尔和贝勒表示这套系统保留了真正的二进制中关键的算术简化，你不用记忆繁琐的记数规律，只需要记住寥寥几条简单规则，比如 2×K=P 和 2×P=T。
研究作者告诉《自然》杂志，虽然这套系统有其缺陷，但“利大于弊”。
文化因素
加州大学圣地亚哥分校的认知科学家拉斐尔·努涅斯（Rafael Nuñez）表示，二进制系统这个构想比曼加雷瓦文化要早。他说“其至少能追溯到大约公元前9世纪的古代中国”，而且能在启发了莱布尼茨的千年古籍——《易经》中找到相关描述。努涅斯还说“诸如玛雅人等另外一些先民，已熟练地将二进制和十进制结合运用，来记录时间和天文现象。因此，曼加雷瓦记数系统的拥有的认知优势或许并不独特。”
即便如此，本德尔和贝勒说，像这样的“混合”系统也并不简单，要创造出来也不容易。“很难想象谁能造出这套系统来，尤其是在这个人口不多的小岛上，”他们说。但他们同时说道：“这一事实同时证明，文化对于数量认知的形成多么重要——比如，在这个案例中，处理大数的方式会如何激发创造性方案。”
努涅斯同意以上观点，同时他补充道，这项研究显示了，“在发明记数系统，以及形成人类数量认知的差异时，文化因素的主导性”。
NASA宇航员拍摄的曼加雷瓦岛的照片 图片来源：Wiki Commons