1、π决定了曲流河的蜿蜒程度
这是π在现实中最惊人的应用之一:一条平原上的河流,它的曲折程度——也就是河道的总长度除以源头到入海口的直线距离——随着时间推移会趋向于π。
现实中没有那么理想的河流,平原河的这个数值更可能比π稍微低一些。但是在数学中没有这个问题——1996年数学家Hans-Henrik Stølum在《科学》上发表论文证明了这一点。
不过这也没那么神秘,想象一下一条由许多圆弧交替拼接组成的河流,就能直觉上理解为何这个数值是π了。
 图片来源:google
图片来源:google
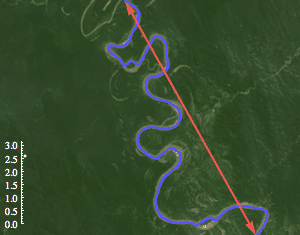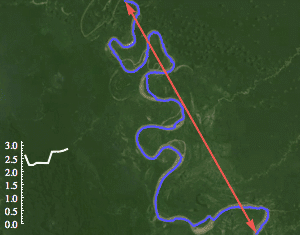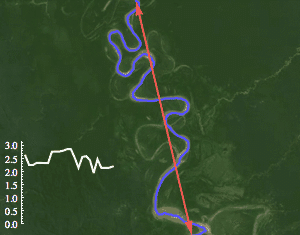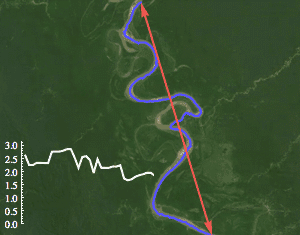 图片作者可能是blog.matthen.com
图片作者可能是blog.matthen.com
下面两张图是作者汉斯-亨里克·斯托罗姆(Hans-Henrik Stolum)用纯粹的数学公式推演出来的河流演化,可以和上图对比一下。
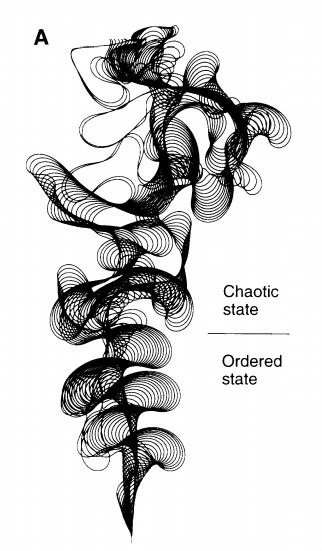
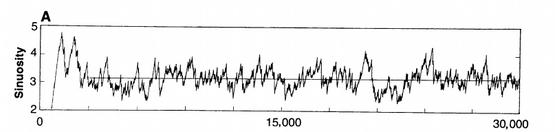
2、π里包含了所有可能的数字组合吗?答案是“不知道,大概吧”
虽然在《疑犯追踪》里宅总有那个著名的演讲,声称π包含了一切,也有很多由此衍生而来的段子(不要在你的硬盘上存储π,因为它侵犯了有史以来所有可能的版权,包含了全世界所有国家的所有最高机密,等等),但这一点并没有得到数学上的证明。再强调一遍,没有证明。我们明确知道π是无限不循环的,仅此而已;剩下的都是猜想。
不过还是有人开玩笑地设计了一套文件系统“πfs”,你的所有的数据都(很可能)存在π的某一个地方,所以不需要你亲自记住这些数据,只要记住这些数据在π的哪里就行了。

3、重力加速度g差一点就是π的平方了
你算过π的平方吗?掏出计算器算一下看看,你会发现它约等于9.87。做过高中物理题的同学可能会意识到,这和地球表面的重力加速度g——9.81m/s^2——在数值上只差一点儿啊。
其实,不但是数值上差一点儿,而且是差一点儿就分毫不差了。

π是没有单位的,所以怎么着都是这个数。但是重力加速度是有单位的,所以如果当年对标准单位定义变了,那这个数也会变。而历史上第一个“米”的定义,就恰好能让π^2和g在数值上相等。
但这算不上是巧合,1668年提出这种方案的英国人约翰·威尔金斯是根据“秒摆”来定义的。所谓秒摆就是从一头到另一头正好花费1秒的单摆(也就是周期为2秒),他把秒摆的长度定义为1米。
那么,根据单摆的周期公式 T = 2π (L/g)^1/2,T=2秒,L=1米,就立刻能够得出g=π^2 m/s^2。听起来是很方便合理的定义公式嘛。
到了1791年,法国大革命期间,法国科学院要设立一种新的度量衡——也就是今天的米制。竞争的双方,就是秒摆定义和地球周长定义。不过最终科学院选择了周长定义——把1米定义为地球子午线长度的4000万分之1。这是因为,当时已经发现重力加速度在地球各个表面是不同的,所以一个秒摆换了地方就不是秒摆了。
不幸的是,这也导致今天的学生面对每道单摆题,都要多花好几个一秒去算数……
 为啥老式挂钟要做得这么长?就是因为它们是设定成秒摆的,需要大约1米长的钟摆。
为啥老式挂钟要做得这么长?就是因为它们是设定成秒摆的,需要大约1米长的钟摆。
不过按照今天的米的定义,标准重力下的秒摆长度只有 0.994 米。
4、我有一个π,我有一个e,嗯~你说啥?
π是无理数,e也是无理数,可是我们竟然不知道π+e, π/e或者lnπ是否是无理数!只知道它们不是八次以下、所有系数都小于10^9的多项式方程的根。
事实上,很多关于π和e的看起来基本的信息,我们都不知道。当然这不是因为π和e本身有多神秘,只是因为和无理数打交道真的是很难。
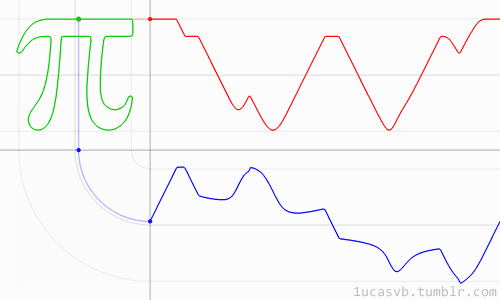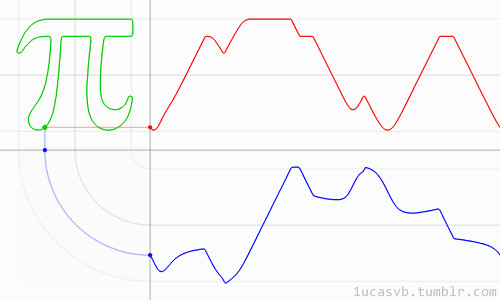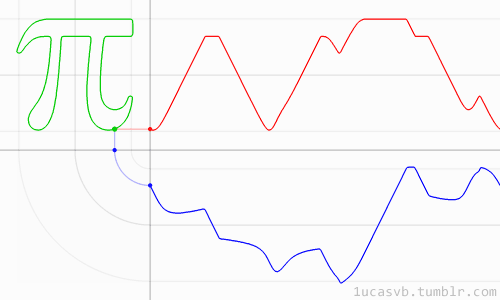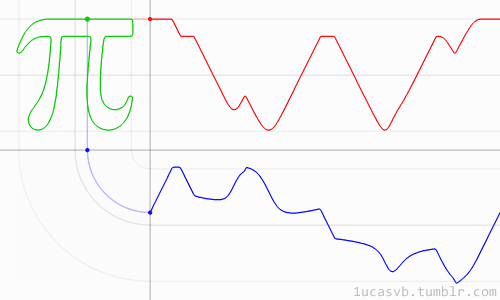 π:我为什么要讲理?
π:我为什么要讲理?
但是至少我们知道,π+e和πe不可能同时是有理数。这个问题的证明留给读者作为练习(对于高中数学学得好的人而言不难)。
顺便说,π自己直到18世纪才被证明是无理数。后来的数学家提出了一些比较简单的证明,最简单的可能是 Ivan Niven的证明(太长了,这里写不下),原则上高中数学学得好的人是可以看懂它的——如果你真的看懂了,请认真考虑报考数学专业。
 i 乱入。然而看懂这幅图只能证明你没有朋友(。
i 乱入。然而看懂这幅图只能证明你没有朋友(。
5、可能是最无聊的数学论战:π是错的吗?
圆的周长被定义为2πr,一个圆的弧度是2π,很多常见公式(比如单摆周期)都有2π,这让一些数学家认为2π才是更基本的常数。一位美国数学家麦克·哈特尔(Michael Hartl) 建立了网站 tauday.com,呼吁人们用希腊字母 τ(tau)来表示“正确的”圆周率 C/r = 6.2831853... 。哈特尔建议大家以后在写论文时,用一句“为方便起见,定义 τ = 2π ”开头,推广这一更为科学的圆周率记号。

支持τ的人建立了τ日(6月28日)来和π日(3月14日)分庭抗礼,每年都会在这两天相互把对方批判一番。不过显然这样的论战对大部分人来说没有意义。正如某位不可考的网友指出的,如果π是错的,τ岂不是两倍的错?
 一个折衷的办法……来源:xkcd.com/1292/
一个折衷的办法……来源:xkcd.com/1292/
6、π被称为π只有很短的历史
虽然人们知道π将近4000年,“π”作为代表圆周率的符号被人们使用却是近300年的事情。1706年,英国数学家William Jones 最先使用希腊字母π表示圆周率。π在希腊字母中排行第十六,也是希腊语“周长”的第一个字母。1737年,瑞士大数学家欧拉也开始用π表示圆周率。
所以,在此之前,他们就不能讲关于π和馅饼的冷笑话了,好可怜哦(画外音:请问谁会有这样的需求啊)
7、π日的历史,就更短了……
最早有记录的π日庆祝活动,是1988年3月14日在美国旧金山科学探索馆一位物理学家Larry Shaw的倡议下,工作人员和游客们在探索馆的圆形空间内举行了庆祝活动,并分享了一个水果派。
2009年3月11日,美国众议院通过了一项决议,把3月14日正式确定为全国的“π日”(National Pi Day)。
8、圆周率出过歌和书(也就算了),居然还出过月刊?
作曲家迈克尔·布雷克(Michael Blake)将圆周率的前31位数字(3.1415926535897932384626433832795...)一个个“翻译”成了音符。他利用勋伯格十二平均律中所引入的半音阶概念,将半音阶与数字一一对应,即令1=C,则3=D,5=E,6=F,依此类推。
这段小小的曲子每分钟节拍数为157,恰为314的一半。由简单的钢琴旋律引入,中途又加入了手风琴、木琴、夏威夷四弦琴等乐器,丰富了整个旋律。戳这里收听→http://v.youku.com/v_show/id_XMjQ5NzIzMDcy.html
出书又是怎么回事?日本有个很迷的社团出版过一本书叫做《円周率1000000桁表》,1996年就开始发售了,至今依然可以在日本亚马逊上买到。
长成这样:
 极具简单粗暴之美_(:з」∠)_
极具简单粗暴之美_(:з」∠)_
后来嫌不过瘾,又出了《自然常数e100万位》、《素数15万个》,以及《月刊圆周率》杂志,每月连载十几万位的π…
 记住这个社团的名字。
记住这个社团的名字。
 ……简直有毛病(╯‵□′)╯︵┻━┻
……简直有毛病(╯‵□′)╯︵┻━┻
好评连载中!想要吗?
顺便说,这个社团在同人展上的画风也非常迷:

9、π总是在最奇怪的地方出现,比如——概率论
在几何问题中,圆周率显然很重要;但奇怪的是,π也驰骋于几何以外的其它数学领域,它在概率问题中的频繁出现让人们得以通过实验模拟估算它的值。(当然,多学一点数学,你就会发现其实也没那么奇怪了。)
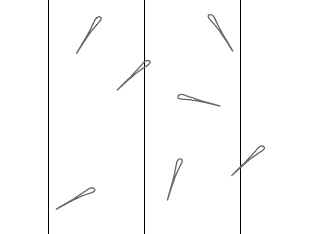
比如鼎鼎有名的布丰投针问题:地板上画一系列间距为2a的平行线,将一根长度为a的针随机投向地面n次,那么针与平行线相交的概率是多少? 1777年,布丰本人给出了解答——相交概率为1/π。很多人甚至依靠此实验推算π 的近似值。1850年,一位叫沃尔夫的人在投掷5000多次后,得到 π 的近似值为3.1596。由投针问题引入的计算 π 的方法,不但因其奇妙而让人叫绝,而且还开创了随机数处理确定性数学问题的先河。
任意两个整数互质的概率是 6 / π^2,基于这一点,英国伯明翰阿斯顿大学的罗伯特•马修斯计算了天空中100颗亮星间的角距离,并把它们转化为100万对随机数字,其中约61%没有公因数。他得到的π值=3.12772,准确率达到了99.6%。
10、派和披萨有一个诡异的联系——除了都很好吃之外
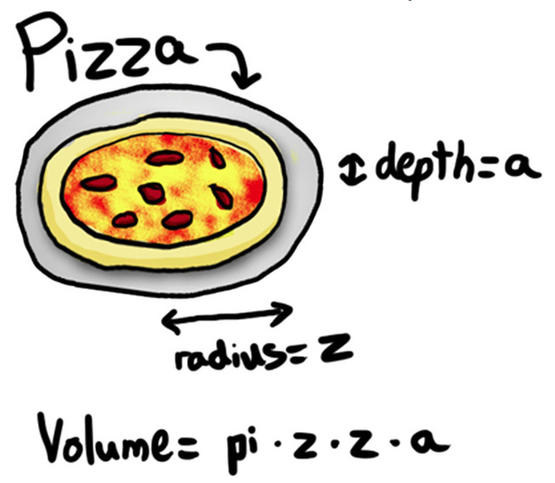
这是一个著名的数学笑话:“一个厚度为a,半径为z的披萨的体积是多少?”答案是:“pizza。”这个结果有时被称为披萨第二定理。当然,这只是圆柱体体积公式的一个简单外推罢了。
11、π出现在据说是最美的公式里,但其实这公式的母体才是最美的
嗯你们知道我要说什么,就是所谓的欧拉恒等式:e^iπ+1=0.

这个公式的厉害之处在于把数学里最重要的5个数——e,i,π,1和0放在了一个等式里。
但是这个公式本身的意义却很有限。它的几何意义不过是说,如果你旋转了π的弧度,那就正好转过了半个圆……这还用你说嘛!
真正厉害的公式不是欧拉恒等式,而是它的母体——欧拉公式:
e^ix = cosx + isinx
欧拉恒等式只是令x=π时得到的一个特例,欧拉公式本身才应该被称为最深刻最美丽的数学公式。比如,利用这个公式可以很容易证明i的i次方是一个实数!
证明么……当然了,留作读者练习之用。(滚走)
12、最后来个实用的:如果你想背π
背到762位就可以了。这是理查德·费曼的著名冷笑话……因为在π的762位,出现了连续6个9,所以他说,你可以背到762位,然后以“……999999,等等”来收尾。
 6个9,不是666666,别背错了。
6个9,不是666666,别背错了。
(编辑:Ent)
