我向来对于高声嚷嚷着“客人至上,服务第一”的口号,有种无法完全信服的感觉。毕竟说起服务这种事情,应该不是以“让客人感受到的程度”为指标。举例来说,逛街时要是专柜小姐一直如影随形地跟在一旁,贴心介绍每一件你只有食指碰到的商品,再拿五种颜色让你试穿,虽然服务周到得没话说,压力却也大得让人没办法说话。最极致的服务,应该要让客人以自己喜欢的方式,从事喜欢的行为,完全察觉不到正在被服务。
就这点来说,我认为可以跟复印机里的A4纸学习服务的精神。
利希腾贝格比例
A4纸是生活中最常用的纸规格。A系列的纸张规格特色在于:
- A0、A2、…、A5,所有尺寸的纸张长宽比都相同。
- A0对裁后可以得到2张A1,A1对裁可以得到2张A2,依此类推。
这两项特色让A系列规格的纸张非常好用,画在A4纸上的图画可以等比例放大到A0海报上。手边只要有某一款A系列的纸,即能做出任意大小的A系列。但事实上不是任意一张纸对裁,都可以得到比例跟原来的纸一模一样的两张纸。只有A系列纸张特殊的长宽比——利希腾贝格比例(Lichtenberg ratio)的特殊比例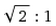 ,才能带来这种特性。
,才能带来这种特性。
举实际的数字给各位看:A4是21厘米×29.7厘米 ,29.7/21 =1.41;A5是29.7/2 = 14.8厘米×21厘米,21/14.8= 1.41;A0是84.1厘米×118.9厘米,118.9/84.1=1.41,都趋近于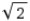 。
。
换句话说,我们都享用了利希腾贝格比例的好处,却很少人知道利希腾贝格比例是什么,某种程度上,这就是最极致的体贴,让人享用到它的好,却察觉不到它的存在。
嗯,我不是在讲女性用品广告台词,虽然两者间很相似(以每一种距离来说都是)。
躲在A4里面,还有更了不起的比例
黄金比例(golden ratio)1.618可以称之为比例之王,不管从Google搜寻或被应用的范围来说,他都是最常见的比例。不过,事实上还有类似黄金比例的比例,和利希腾贝格比例一样隐藏在A4纸里面,名字刚好跟《圣斗士星矢》里圣斗士的阶级相同,是黄金圣斗士之下的白银圣斗士,不,白银比例(silver ratio)——2.414。只要以A4纸的短边为边长,划出一个正方形并裁掉,剩下长方形的长宽比即是白银比例。我们可以验证一下,A4纸的长宽比是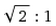 ,用短边划出正方形并裁掉后,剩下长方形的长宽比将会是1: [
,用短边划出正方形并裁掉后,剩下长方形的长宽比将会是1: [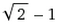 ] = 2.414。
] = 2.414。
我们也可以把白银比例表示成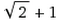 ,它和(
,它和(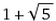 )/2的黄金比例有许多相似之处。例如,他们都和某个数列有关。先前介绍过黄金比例和费波那契数列(Fibonacci series):1、1、2、3、5、8、13、21、…。后一组数字除以前一组数字,便可以得到近似于黄金比例的比值。白银比例则用上了佩尔数列(Pell series):1、2、5、12、29、…。拿前后两组数字相除,可以得到2、2.5、2.4、2.41、…越来越接近白银比例2.414。我们可以用图形的方式来解释,为何费波那契数列和佩尔数列中产生黄金比例或白银比例。
)/2的黄金比例有许多相似之处。例如,他们都和某个数列有关。先前介绍过黄金比例和费波那契数列(Fibonacci series):1、1、2、3、5、8、13、21、…。后一组数字除以前一组数字,便可以得到近似于黄金比例的比值。白银比例则用上了佩尔数列(Pell series):1、2、5、12、29、…。拿前后两组数字相除,可以得到2、2.5、2.4、2.41、…越来越接近白银比例2.414。我们可以用图形的方式来解释,为何费波那契数列和佩尔数列中产生黄金比例或白银比例。
首先,费波那契数列的第n组数字是前两组数字的和,意即Pn = Pn-1 + Pn-2,例如21=8+13。佩尔数列的第n组数字前一组数字的两倍加上再前一组数字,意即Pn = 2Pn-1 + Pn-2。例如29=12×2+5。再将费波那契跟佩尔数列的递归表示法除以Pn-1,可以得到
Pn/ Pn-1 = 1+ Pn-2/ Pn-1。
Pn/ Pn-1 = 2 + Pn-2/ Pn-1。
第一个式子表示,大的黄金比例长方形是一个正方形加上一个小黄金比例的长方形。
第二个式子则是,大的白银比例长方形可以由两个正方形,加上一个小的白银比例长方形组合而成,如下图所示。
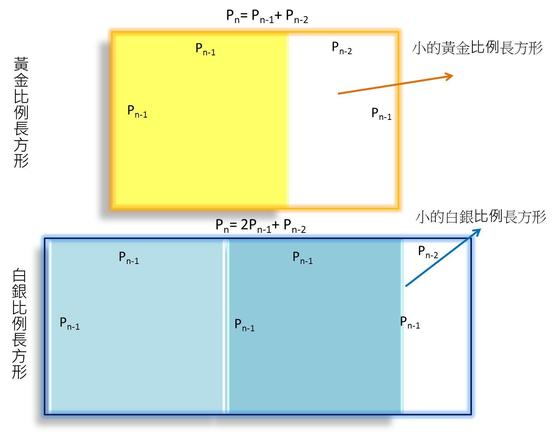 图示由作者提供。
图示由作者提供。
白银比例的服务精神
利希腾贝格比例让纸张的使用更加便利,黄金比例跟白银比例的用途更广泛,其中之一是在艺术上的贡献。例如下面的绿色菱形,对角线的长宽比刚好是白银比例,因此可以用方才的几何规则“两个大的加一个小的”,将三个这样的菱形,其中两个横放,三个并排,制造出一个等比例放大的蓝色菱形,放大的比例刚好是白银比例。
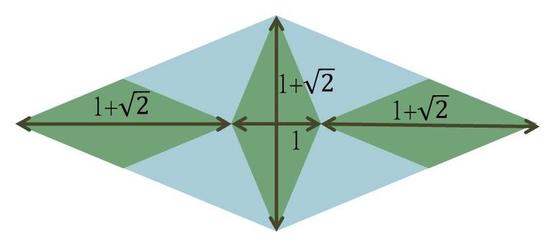 图示由作者提供。
图示由作者提供。
这种特殊的菱形与正方形,是下图复杂的伊斯兰风格拼贴镶嵌的基本元素。
 图示由作者提供。
图示由作者提供。
比起一般地板磁砖的正方形,或蜂巢状的六角形镶嵌,这种镶嵌更华丽美观。这么复杂的镶嵌,除了基本构成的菱形需要白银比例,镶嵌过程也需要用上白银比例,最后构成的众多正八边形里,依然也有白银比例。
可以看见,白银比例一样提供了最佳的服务,让使用者察觉不到,却因为它获益良多。最起码豪宅里使用了这种镶嵌技术(Ammann-Beenker tiling)的土豪一定不知道背后有白银比例,不然他铁定会把设计师叫过来臭骂一顿:
“为什么不用黄金比例,要用白银比例呢?!”
有噢,有黄金比例的镶嵌,称之为彭罗斯拼图(Penrose tiling),数学可是最有服务精神,服务最周到的科学了。
