瑞士与法国、德国边界有个人口很少超过20万的小镇巴塞尔,是个在科学意义上非常著名的地方。那里有瑞士最古老的大学(建于1460年),在那里出生和工作过的杰出人物不计其数,包括大名鼎鼎的贝努里家族和史上最伟大、最多产的数学家欧拉。不过,我们这里要说的是一个中学老师,他把玩一组四个数据得到的公式是量子力学得以发轫的基础事件之一。
巴尔末1825年出生于巴塞尔,1849年在巴塞尔大学获得数学博士学位,也算是个早慧之人。巴尔末一生都是在巴塞尔度过的,他一直在一所女校里教书,间或也到巴塞尔大学上课。巴尔末老师研究数学,但是到了60岁也没有什么值得称道的成就,看来他这一生大概会碌碌无为了。可是就在1885年巴尔末老师60岁时,他在盯着一组四个数字足够长时间后,得到了一个可以给出这四个数字的公式,这个公式让巴尔末老师的名字深深地刻在了物理学史的纪功碑上。
天上的太阳慷慨地把光线撒到大地上,燃烧着的物体也会发光, 到1885年,科学家关于谱线的研究已经获得了一些非常深刻的认识。
比如,人们注意到碱金属的谱线很有规则,某几条谱线从分布上看明显属于一组(看似趋于一个极限值)。那时,关于谱线的波长也有了精确的测量数值,氢在可见光范围的四条明亮谱线的波长分别为6562.10(红色),4860.74(水绿色),4340.10(蓝色)和4101.20(紫 色),单位为10-8 cm(图1)。巴尔末老师发现这四个数是3645.6的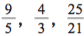
和
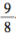倍(这是个趋于1的数列)。那这四个分数
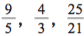和 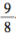有什么奇特的地方吗?有!它们分别是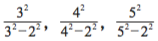
和，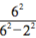
,或者说是一般表达式
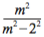的 m = 3,4,5,6 的四种情形。也就是说,如果这四条谱线真的来自一个线系或曰家族,描述它们之间关系的公式就在这儿。那么,m = 7呢?可以算出它对应的波长约是3969.6,而在这个地方竟然确实有氢的一根谱线,只是这是一条弱的紫色谱线(或者紫外线),不易看清而已。巴尔末老师的公式,隐隐地让人们觉得还有大用。
后来,里德堡(Johannes Rydberg)参照巴尔末老师的公式,给出了谱线波长的倒数(现在被称为波数)的一般表达式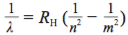 
，其中RH是里德堡常数，n 和 m(> n)都是常数。巴尔末老师的公式只是里德堡公式的 n = 2 的特例。
人们从里德堡公式能看出什么呢?这个公式最具内涵的地方,或者说是通向自然奥秘的地方,是它是两项之差。设想你从一个台阶往下跳到另一个台阶,你的落差就是台阶的高度差,你若是摔到台 阶上,估计你的尖叫声的频率会正比于这个落差。1911—1913年间,一个丹麦人玻尔把原子的发光过程理解为电子自一个能量台阶到另一个能量台阶的跳跃(我们的中文物理学故意将之翻译成文绉绉的 “跃迁”)引起的,台阶之间的能量差就是光谱线对应的能量。如果这个解释成立的话,那就要求电子有稳定的能量台阶(这一点好办,我们可以简单 地假设它必须这样就行,且稳定的能量台阶对应的能量应该包含一个正比于整数平方倒数的项。如何做到这后一点呢?在1913年,人们能求助的就是经典力学了。经典力学里有遵循平方反比律的引力, 有牛顿力学已经成功解决的太阳系轨道问题。可以将氢原子这个电子–质子的体系类比于行星–太阳的 体系,行星–太阳体系的经典力学问题是清楚的, 体系的能量(以及能量如何决定行星的轨道)、角动量是有公式表达的。如果要将这样的体系的能量 限制为正比于整数平方的一些孤立的值,能通过什么限制条件实现呢?除了角动量,还能有什么选择呢?于是,玻尔假设电子稳定能量台阶对应之轨道的角动量是普朗克常数(真巧,普朗克常数的量纲 就是角动量的量纲)的整数倍,即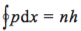 
，此即 为所谓的玻尔量子化条件,玻尔惊奇地发现得到的轨道能量竟然正比于 
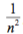，也就是说,只要假设轨道的角动量服从玻尔的量子化条件,那么所得到的轨 道能量的表达式就能给出氢原子光谱线(对应的能量,或者波长,或者波数,或者频率)。提醒各位读者,玻尔这里用到的n其实是薛定谔那里的l 。
等到1926年薛定谔方程出来了以后,玻尔关于氢原子的行星–太阳模型就显得太简单了些,但是玻尔引入的静态轨道和跃迁的概念却在量子力学中保留了下来,实际上,跃迁是量子力学的关键性基础概念之一。薛定谔的波动力学揭示了氢原子中电子轨道(能量)的更多秘密;海森堡的矩阵力学尝试去理解谱线的强度,发现谱线强度取决于跃迁过程涉及的两个轨道的某些性质。1926年,关于光的研究也取得更多进展,有了有别于此前的“光的能量量子”的光子概念。从此,量子力学的发展一发不可收拾,伴随而来的谱学技术和群论的发展更在人 们的意料之外。
巴尔末这位中学老师对量子力学建立的贡献,鲜有文献给出中肯的评价。其实,就算是量子力学文献中总要提及的普朗克,对其贡献的评价也未能说到点儿上。物理学是一条思想的河流。欣赏这条闪光的智慧河流,除了敬畏心,还要在知道更多细节的基础上慢慢品味。
本文为作者授权，引自《一念非凡——科学巨擘是怎样炼成的》
参考文献：
- S. Sternberg. Group Theory and Physics. Cambridge University Press, 1994: Appendix F.