传说骰子的发明人是三国的曹植,为了占卜之用,后来作为赌具流行。其实,数学家们曾依靠掷骰子的实验研究了概率论中一个最重要的定律,大数定律。但令人惊奇的是,就连大自然也会掷骰子,不同的是,它是通过掷骰子选择生命延续的方式。
从投针到掷骰子
1777年,法国数学家蒲丰发明了一种稀奇的计算π的方法:随机投针法。他在平面上画一组间距为D的平行线,将一根长度为 L( L
之所以可以用随机实验处理这个确定性的数学问题,是因为数学家在经过大量独立重复试验和统计大量同类数据之后发现,某一事件发生的频率趋于一个稳定值。这就是数学概率论中的大数定律(Law of large numbers)。当试验次数足够多的时候,事件发生的频率趋于稳定,偏差几乎为零。
让我们举一个直观的例子:掷骰子试验。因为掷骰子的结果符合二项分布,容易算出掷骰子的期望值是3.5,根据大数定律,它就应为实验最终得到的稳定值。事实也确实如此。
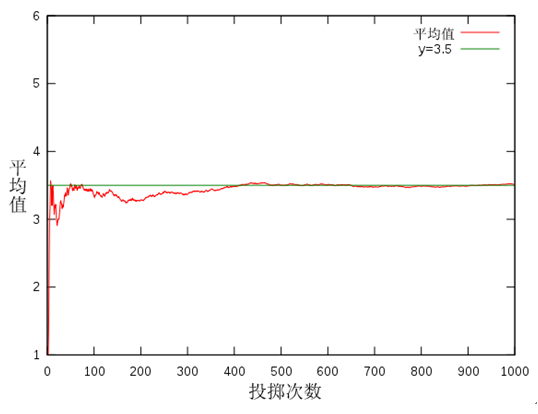
随着投掷次数的增加,骰子的平均点数趋于3.5(图片来自维基百科)
细菌掷骰子吗
爱因斯坦曾说,上帝不掷骰子。上帝掷骰子吗?这是20世纪量子力学留下的一个谜题,我们暂且不论。但让人惊奇的是,就连自然界的万物,也会经常掷掷骰子。
设想这样一个理想化的试验。在一个盛了足量营养液的培养皿里,生活着几千只细菌。这些细菌体内的基因除了某个位点其他全部相同,而这个位点上的基因由 A 和 B 构成, A 、B 各自的基因频率均为 50% 。刚开始,这群细菌在“桃花源”里毫无压力地繁衍后代,数量急剧增长。但是好景不长,随着营养液内水分的蒸发,培养皿开始渐渐枯竭,导致细菌大量死亡,最后只剩下了四只细菌。种群数量大幅度减少的事件,在自然界时有发生,生物学上称之为瓶颈效应。
不妨来看看最后四个幸存者在那个特殊位点上的基因情况吧,有如下16可能:
{A,A,A,A} {A,A,A,B} {A,A,B,A} {A,A,B,B}
{A,B,A,A} {A,B,A,B} {A,B,B,A} {A,B,B,B}
{B,A,A,A} {B,A,A,B} {B,A,B,A} {B,A,B,B}
{B,B,A,A} {B,B,A,B} {B,B,B,A} {B,B,B,B}
因为 A 和 B 是等可能存在的,所以上述16种情况每一种情况出现的概率均为 1/2 * 1/2 * 1/2 * 1/2 = 1/16 。我们再根据 A 、B 在集合中不同的数量进行划分,得出下表
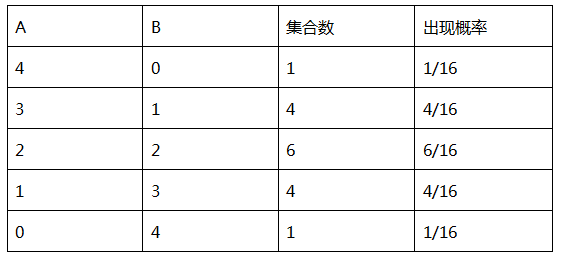
从上表中我们可以看到, A 和 B 基因频率相同(即数量相等)的概率只有 6/16 ,而 A 、B 基因频率不相等的概率却有 10/16 。初始时 A 和 B 的基因频率是相等的,而现在 A 和 B 的基因频率更倾向于不相等,且有12.5%的概率使得等位基因A或者B在这一代彻底消亡。由于不可抗拒的力量让种群数量急剧下降时,细菌开始掷骰子般地作出选择,使得基因频率大幅度改变,某一基因倾向消失(另一相对基因倾向固定)。这就是遗传漂变,在生物遗传学中,瓶颈效应将有可能导致遗传漂变。
寻找“掷骰子”的真相
为什么会这样呢?让我们来简单地分析一下。
很明显,试验中细菌在那个位点上的基因的遗传规律符合概率论中二项分布,我们先用二项分布对这一假想实验进行描绘:
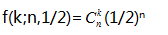
其中n表示细菌的数量,k 表示等位基因 A (或者 B )的数量, 1/2 是等位基因A和B的基因概率。当 n 值足够大时,根据大数定律,只要细菌的繁殖数量始终保持在这一数量级上,那么基因A和B的频率将保持恒定,即初始的 50% 。但当细菌大量死亡,比如本例中所举的一个极端,最后仅幸存四只的话,那么显然已构不成“大数”,就会和上述掷骰子试验投掷次数小于100的情形一样,基因频率将呈现出极大的波动。
这一分析同样适用于所有动物。实际上,研究表明自然界里几乎所有的生物都遵循这个规律。
用死理性派的眼光看自然
目前自然界中很多生物濒危的原因都与瓶颈效应造成的遗传漂变有关。例如2002年的一份 研究报告 就指出,大熊猫在4.3万年前遭遇瓶颈效应,种群数量急剧下降,是使其陷入今日绝境的主要原因。物种的某个或某些基因永久消失,其实质是降低了该物种的遗传多样性。而遗传多样性越高,就越有利于族群的生存及演化。大熊猫本身生育率低,对生活环境的要求又高,种群在遭到重创后,遗传多样性贫乏,在野外更难存活。再加之19世纪末和20世纪初国内外人士对大熊猫的猎杀和对其栖息地的破坏,使得大熊猫的生存现状雪上加霜。直到1958年四川卧龙自然保护区的建立,大熊猫的生存才在一定程度上得到了保障,数量也开始逐年增加。
虽然如此,但大家在读完本文后也不必要走入另一个误区,认为种群数量越少,则遗传多样性也越低,或遗传多样性越低,则其种群数量一定很少。其实这二者虽有相关性,却没有必然的因果关系。比如川金丝猴濒危程度也比滇金丝猴小,但实际上滇金丝猴的遗传多样性并不比川金丝猴低。而国二级保护动物穿山甲,它的遗传多样性甚至要高于家猪。
