“从前,有个人娶了三房姨太太。后来,他死了。” ——《麦太太睡前故事集》
麦太太的故事结束了,但是死理性派的征程才刚刚开始。话说那位老兄留下了遗嘱,三个姨太太分别可获得100、200、300元的遗产。但清算之后才发现,那个倒霉蛋留下的钱根本不够分……
实际上,这个故事早在犹太人典籍《塔木德》中就有记载。《塔木德》,作为犹太教仅次于《圣经》的经典,记载了犹太人传统口耳相传的生活习惯。是一本有关律法条例、传统习俗、祭祀礼仪的论著和注疏的汇集。
这部典籍的主要部分成书于2世纪到6世纪初,而令人称奇的是,那时的犹太 拉比 们就已经具备了出色的博弈论知识。不妨看看聪明的犹太人是如何人性化地解决这个难题的。
诡异的分配方案
根据《塔木德•妇女部•婚书卷》第十章第四节,“塔木德解决方案”如下:
| 一房 | 二房 | 三房 | |
| 遗产为100元 | 100/3 | 100/3 | 100/3 |
| 遗产为200元 | 50 | 75 | 75 |
| 遗产为300元 | 50 | 100 | 150 |
按通常逻辑,这三人得到的遗产比例应为1:2:3,而在犹太先哲们的裁决中,只有在遗产数为300元的情况下这一比例才成立。没有人可以解释为什么,这个奇怪的方案也就成了千古之谜。
解铃还须系铃人,《塔木德》的解释
直到1985年,两位数学家才解决了这个问题。他们惊奇地发现塔木德解决方案竟完全符合现代博弈论的原理!
解决这个问题的数学家注意到,这个难题就在《塔木德》中留有一条提示。在《损害部•中门卷》第一章第一节中记载了这么一个故事。甲、乙分一件大衣。甲说:“大衣是我的!”,乙也说“大衣是我的!”这时,大衣两人各分一半。如果甲说“大衣是我的!”,乙说“大衣有一半是我的”,那么,甲分到 3/4,乙分到 1/4。
这个解决方案看上去也不同寻常,但对此,数学家们已有一个比较好的解释,被称作“争执大衣原则”:将总财产分为“有争议”和“无争议”部分,无争议部分财产直接分给声明者,争执双方再平分争议部分财产。 对于声称拥有一半大衣的乙来说,显然另一半并不属于他,因此只能和声称拥有全部大衣的甲平分剩余的一半。
如果《塔木德》全书秉承相同的财产观,那么“三妾分产”问题有没有可能是争执大衣原则在超过两人的情况下的推广呢?
分配方案随财产数量变化
事实也的确如此。不妨先来看看2个人按照争执大衣原则分配财产时,每人所分到的随总财产变化的情况。设甲与乙分别要求获得的财产为 c [ 1 ] 、c [ 2 ] (设甲索求较少,即 c [ 1 ]
当E 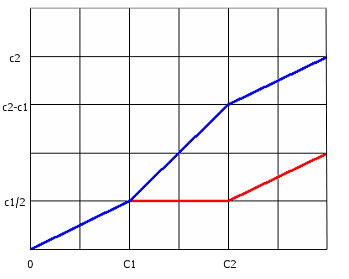
按照争执大衣原则两人分配
将甲、乙二人所得画成折线图如上。可以看到,当 E 不大时先两人平分,然后增长的部分只分给乙,当乙拿到一定份额时总财产继续增长的部分由两人平分。
多人争执时的财产分配
接下来我们就将这种分法推广到多人时的情形。记所有参与者要求的财产按从少到多分别为 c [ 1 ] 、 c [ 2 ] … c [ n ],总财产 E 从 0 开始慢慢增加。当 E 很小时,将 E 平均分给所有参与者,直到各方都拿到 c [ 1 ]/2 ,此时停止继续给1号参与者分配财产(记他为1,其余参与者分别记为 2 、 3 … n )。当总财产继续增加时,将增加的部分分给剩下的 n - 1 人,直到所有人都恰好拿到自己声明值的一半。此时各位参与者的声明值之差(即他的损失)恰为他要求值的一半。当 E 继续增加时,则将增加的部分分给n,直到他的损失与第 n – 1 位参与者相同,再接着将增加的部分平分给要求 n 和 n – 1 ,直到 n 的损失与 n-2 相同,再将继续增加的部分分给 n 、n - 1 、 n - 2 …… 直到所有人都分得自己所要求的份额为止。
回到最初的“三妾争产”这个案例上来。根据上述分析,我们可以画出按照这一方案分配财产情况的折线图。
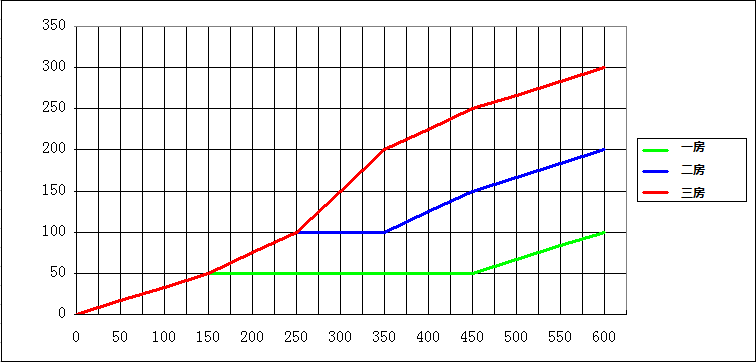
按照争执大衣原则“三妾分产”财产分配情况
可以看到,这一分配方案与《塔木德》中关于“三妾争产”的记载是吻合的。至此,我们就解决了这一千古难题。
塔木德方案的经济学意义
但是,且慢。这种复杂的分配方案有什么意义呢?其实,相比按比例分配而言,在总财产较少的情况下,塔木德方案的天平是向弱者倾斜的。在资源不足时,优待弱者十分重要。
举个例子,来看看将塔木德解决方案应用到现实社会的破产决算纠纷,会出现什么情况。假设有家大型商场破产了,它的供货商,甲、乙均是大公司而丙是一家小工厂,现分别要求获得 300 万、200 万和 100 万元的债务补偿。由于破产的公司往往都是严重的资不抵债,因此可以认为这种情况下总财产较少,此时塔木德解决方案就能比现行的按比例分配方法更好地保护小户的基本利益。对于大公司来说,少收回一些债务只是减少一些盈利;但对于小厂来说,按比例进行破产决算则可能意味着因亏损过大倒闭。现实生活中也往往如此,当一家企业倒闭时,受灾最重的不是大供货商,而是中小企业。而一旦这些中小企业连锁倒闭,那么整个区域的经济都会遭到重创。因此,在破产决算中保护这些中小企业的利益才是最关键性的环节。
回到三妾争产的故事,假如这三位妻妾都要靠遗产来生活的话,那么塔木德解决方案对于一房这样的穷人来说就是决定性的。假如采用按比例计算来分配遗产,那一房因为分到的遗产过少,也许很快就会流落街头。这也正是塔木德解决方案的社会价值所在。
奇妙的是,这个方案在保护了弱者的利益的同时仍然保持了博弈规则的公正性。从整个破产决算游戏来看,如果应用塔木德解决方案作规则的话,那么大户小户都有胜出的机会,而且至少从理论上说,双方胜出的机会是相等的。因为如果财产数目超过负债额一半的话,则大户可以分得较多财产,否则小户分得更多。这种公正性可以在很大程度上也保证各方玩家对规则的尊重。
参考资料
[1]张平, 三妾争产续谈:塔木德解决方案的经济社会意义
[2]姜启源,谢金星,数学建模案例选集,高等教育出版社,2006
[3]姜启源,谢金星,叶俊,数学模型(第三版),高等教育出版社,2003
[4] R. Aumann, M. Maschler. Game-theoretic , analysis of a bankruptcy problem from athe Talmud, J. of Economic Theory, 36 t (1985), 195-213.
[5] W.Thomson. A xiomatic and game-theoretic analysis of bankruptcy and taxation problems: a survey, Mathematical Social Sciences, 45 (2003), 249–297.
