抢占正方形

这是一个双人对弈的游戏，道具很简单，纸和笔就行。规则也不复杂，首先游戏者要在纸上点出一些矩形点阵，如下图所示，矩阵的大小没有限制。

之后双方轮流选取两个相邻的点，用水平或者垂直的线段将它们连起来（每两点之间只能连一次）。如果某个 1×1 的小正方形（以下称为小方块）的 4 条边都被连上了，那补齐这个小方块的一方就获得 1 分（在这个封闭小方块里写一个代表玩家的字母表示得分），得分的玩家被奖励多走一步，再连一条线。在所有可连接的线都连完后游戏结束，得分高的一方获胜。如果共计有偶数个方块，最终双方得分相同，算后手的玩家赢。

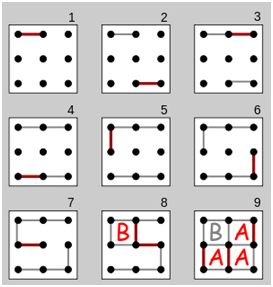
对新手来说 3×3 的点阵比较合适，高手之间推荐玩 7×7 的点阵。不妨来看个简单的例子，上图其实就是 3×3 点阵的一个游戏过程：后手的人每次都做出与先手对称的操作，企图把点阵平分成两部分，两个人得到相同数量的方块，最后依靠后手取胜。然而在第 7 步时，先手者补齐了左上角那个方块的第三条边，做出了一个 让步 的操作。对方果断上钩，立刻放弃了对称操作，补齐了左上方块得到 1 分，但与此同时他必须再操作一次，连上一条新的线。在这条线的帮助下，先手的人在第 9 步连续补齐了 3 个方块，赢得了胜利。

到这里，你已经明白这其实是一款策略性很强的游戏。用什么样的策略才能让自己取胜？在回答之前，我们再来看一个例子。

假如面对 1 这种情况，你会怎么办？

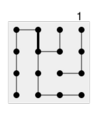
如果像 2 这样操作，把所有可以取得的 4 个方块都拿走，那么对方将拿走剩下的5个方块，于是你输了。

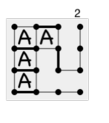
更高明的方法是像 3 这样，只取走 2 个方块，剩下 2 个留给对手。如果对手拿走你留下的 2 个，你就可以拿走剩下的5个。如果对手不拿留下的这 2 个，那你就能拿走所有方块，不管对手怎么操作都是你胜利。

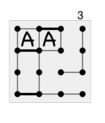
这种“在所有可以取走的方块中留下 2 个，剩下的都取走”的策略叫做“双十字策略”。在详细说明双十字策略之前先介绍一个概念： 链 。在开始阶段，由于没什么限制，连线的选择基本是随机的，唯一要注意的是避免补上某个方块的第三条边。 一直持续这样操作就会使得所有剩下的方块变成一些链，也就是一些只补上了 2 条边、 连在一起的小方块， 它们会因为补上任何一条连线而让对手得到这条链里所有的小方块 。 1 中就有一条长度为 4 的链和一条长度为 5 的链，而长度为 4 的那条链已经被操作过了。

要说的是，不管链中有多少个方块，双十字策略都可以使用。只要链足够长，链中方块的个数大于 2，在之前每个的链中舍去 2 个方块，而在最后一个链里拿走所有方块的策略总是可以赢。因此，两个高手较量时，焦点便是谁能让对手操作第一个长链（给这个长链的某个方块补第三条边）。对一个不懂让步意义的对手，高端玩家只需要做出足够的让步就能“捕获”他。如果对手知道让步所包含的阴谋，高玩则必须在游戏初始阶段控制对手可以做出的让步数量，迫使对方第一个操作长链。

为什么控制可以做出的让步数量就能迫使对方第一个操作长链？因为在游戏中没有理由不去接受一个让步。正如上面 3 的分析一样，如果不接受让步，对手可以很轻松地、没有任何损失地拿回这个让步（并最后获胜）。因此让步总是要接受的，真正要考虑的是接受让步后怎么办。因为对手总要接受让步，所以设计好巧妙的让步就能迫使对方操作第一个长链。

但双十字策略并非无敌。经验丰富的玩家可以通过游戏早期的操作将方块分割来避免这种利用链的策略。只要链的长度不够长，双十字策略就没有什么用武之地了。

当然，正方形点阵还是比较轻松的，如果你已厌倦在矩形，也可以试试在三角形和六边形的点阵里重新激活自己的大脑。

画个圈圈绕死你

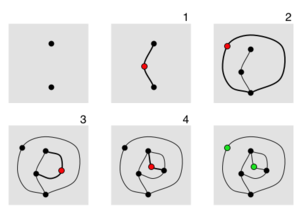
上面的方方正正你还能算的过来，下面这个光是数点你可能就乱套了。它叫做“Sprouts”。实际上，这个游戏的规则和上面一个同样简单，纸上随便点上几个点（但不要点太多，否则耗时太久）。双方轮流用一条线连接某两个点，或者从某个点开始画一个环连回自身，完成连线后再在这条线上加个点。操作过程中需注意以下事项：

用直线或者曲线连接都可以，但是连线不能碰到自身（打结）或者其他的线

新加上的点不能在两个端点上，因此这个新的点必定把新的连线分成较短的两部分

每个点最多只能连接 3 条线，连到自身的线算 2 条线

无法继续进行操作的玩家输掉游戏

让我们来看一个实际的例子。上图展示了有 2 个初始点的游戏过程。经过 4 步操作后，大多数的点都 死了 （已经连接了 3 条线），还剩两个绿色的点依然 活着 ，但根据游戏规则，这两个点再也不能“在一起”了。因此先手的人输了。这些在游戏结束后依然活着的点称为 幸存点 ，它们在游戏中的作用至关重要。

看起来游戏好像永不会停止，因为每一回合都新增加了一个点。但是当我们从 命 的角度来看的话，游戏就显然会停止了。 命指的是每个点还可以连接的线条数 ，比如说初始的点有 3 条命，上图中的红色点都只剩下 1 条命，死了的点（黑色点）就没有命了（废话）。对于每一步操作，连接 2 个点会消耗 2 条命，而新增 1 个点只会增加 1 条命，所以每次操作都会减少 1 条命。假设最开始有 n 个点，一共就有 3n 条命，当游戏一共只剩下一条命的时候（也就是连接了最后两个幸存点），游戏肯定结束了。也就是说，这个游戏在 3n-1 个操作之内必定结束。

这个游戏有必胜策略吗？

既然可以在 3n-1 步内结束游戏，那可以算出这个游戏至少可以持续多久吗？可以，用类似的思路，我们可以分析出这个游戏至少可以持续 2n 步。分析前先介绍一个概念: Pharisee 。

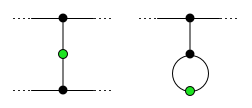
当游戏结束时，每个幸存点（上图绿点）一定刚好有两个死掉的相邻点（上图黑点）。任何死掉的点都不可能与 2 个不同的幸存点相邻，否则将会有一个操作可以连接这 2 个幸存点。 那些与幸存点不相邻的死亡点称为Pharisee ，简称 P点 。

假设游戏有 n 个初始点， m 步之后游戏结束，游戏结束时有 p 个 P 点。就会有

n + m = 3n - m + 2（ 3n - m ） + p

怎么理解这个等式呢？先来解释一下各个小式子。

n+m ：每个操作会新增一个点，于是游戏结束时所有的点有 （n+m）个。

3n-m ：游戏结束时每个幸存点肯定都只剩下1 条命（若某个 1 个点有 2 条命，它至少可以做出连接到自己的操作，这时游戏未结束）。而从之前的分析我们又知道，游戏结束时一共剩下 3n - m 条命，所以游戏结束时幸存点的个数是 3n - m。

2（3n-m） ：每个幸存点与 2 个死亡点相邻，于是与幸存点相邻的死亡点的个数为2（3n-m）。

整个等式的意义就是

在游戏结束时所有的点 = 幸存点 + 与幸存点相邻的死亡点 + P点

将上式整理得到

m = 2n + p / 4

所以游戏结束时至少会进行 2n 步，而且 P 点的个数总是 4 的倍数。

游戏输赢取决于游戏进行了奇数步还是偶数步，而 p 点的数量决定了整个数字是奇是偶，所以实际上博弈的焦点就在于要创造 p 点还是避免 p 点被创造出来。其中一方会试图将幸存点包含在一个封闭的区域内，减少 P 点的个数，这将导致游戏结束的步数减少。而另一方会试图增加 P 点的个数，这又会导致游戏结束的步数增加。

其实这个游戏有四个很重要的特征：

二人对弈

双方交替操作，能够进行的操作是有限的、可枚举的

操作只取决于当前状态，与之前的操作、操作的人或者随机因素无关

某方无法操作则输掉游戏

因此这个游戏是一个组合游戏（Impartial Combinatorial Games，简称ICG）。组合游戏里有两个很重要概念： 必胜态 和 必败态 ：

●那些无法操作的状态都是必败态

●可以移动到必败态的状态都是必胜态（因为当你面对这个状态时，你就可以将这个状态变成必败态交给对手）

●只能移动到必胜态的状态也都是必败态（因为你面对这个状态时怎么操作对方都会面对必胜态）。

只要局面不出现重复，我们就可以用倒推的方式计算出某个状态是必胜态还是必败态。所以，只要给定了 Sprouts 游戏的初始点数，就必定存在一个完美策略使得先手必胜或者必败。这个完美策略可以通过博弈树（用来描述必胜必败态之间的转移）来找到。但是 Sprouts 游戏只有在点数很少的时候才能手动计算博弈树（不信的话你试看看）。

在 1982 年出版的一本叫 《Winning Ways for your Mathematical Plays》 的书中有人用了47页纸来证明初有 6 个初始点的 Sprouts 游戏是必胜的。直到 1990 年，卡内基•麦隆大学的 David Applegate 、 Guy Jacobson 和 Daniel Sleator才使用当时最好的计算机将必胜必败的证明发展到了 11 个点。 3 人通过观察，猜想当初始点个数除以 6 的余数是 3、 4、 5 时先手是必胜的。

后来到 2011 年，这个证明终于推进到了 44 个点，另外初始点数为 46,47,53 的结果也已经证明。到目前为止所计算出来的结果均符合上面的猜想。

不过既然用计算机计算必胜必败态都这么麻烦，那在实际游戏中就不用担心某一方知道必胜策略而导致游戏不平衡了。点上6个点，开动你的脑筋吧！

---

主要参考资料：

[1] 维基百科： Dots and Boxes

[2] 维基百科： Sprouts (game)