地平线离我们有多远

如果地球是平的，理论上你可以看到世界的尽头（如果平坦的世界有尽头的话）。但地球是个球，脚下的大地并不平，远方的大地最终会向下弯曲，落到视平线之下。所以即便天气绝佳、前方一片开阔，你最多也只能看到——地平线。问题是，地平线离我们有多远？实际上所谓地平线，就是我们的视线和地球的切点。如果没有障碍物，“地平线”和我们的距离如下图所示：

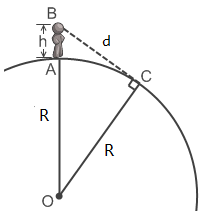
其中 C 点是视线最远端。 R 表示地球半径，这里取 R = 6371 km，h 是一个正常人的视线高度，不妨设为 1.7 米。根据简单的几何知识，很容易算出：

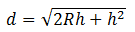
将之前的 R = 6.37 × 10 ⁶ m 与 h = 1.75m代入，可以得到：

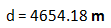
也就是说一个1.75米高的人，在没有遮挡的情况下，能够看到的“地平线”距离他有4.65 km远。当然这只是一个简单的估算，但结果的精确度已经足够。一个平均身高的人站在一望无垠的草原上，那远方的地平线离他不到 5 千米！

欲穷千里目，要上几层楼

地平线没有想象中那么远，欲穷千里目，只有更上一层楼了。不过话说回来，“上一层楼”到底能穷几里目，“穷千里目”又要上几层楼？不妨让我们也来算一算。

上面这句家喻户晓的名句出自王之涣的《登鹳雀楼》。鹳雀楼在公元 1272 年毁于战火，其高度已无从可考，现在的是 2002 年重修而成。我们不妨拿这座高73.9米共九层的新鹳雀楼来计算一下。为了方便，假设鹳雀楼的一层和地平线平行，而其余每层都等高，第九层的房顶也计入整个楼的高度。

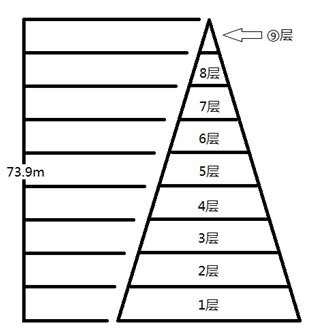
这时平均每层高 73.9÷9 = 8.2 米，加上之前一个正常成年人的视线高度（1.7米）。我们可以得到，当一个人站在第 x 层的时候，他的视线离地面的高度为

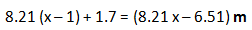
这个高度就是上一部分计算地平线离我们有多远公式 d=√(2Rh+h^2 )中的 h。代入则有：

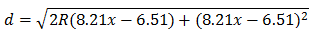
将x=1, 2, …, 9及R=6371000代入，可得：

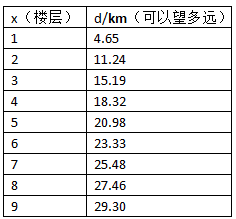
其中 x 是楼层数，而 d 和前文中例子提到过的含义一样，表示在当前楼层上站着的人可以望到的最远距离。每当我们“更上一层楼”的时候，视野范围都会扩大若干公里，但扩张的速度却越来越慢。

如果认为诗中的“千里”就是500 km，根据之前的公式，把 d = 500000 代入可以算出:

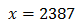
也就是说我们需要上到2387层高的楼，才可以“穷千里目”（这里是一个简化计算，没有考虑光的折射问题）。要是真有这样的一座高楼，它的楼顶距离地面足足有 20 公里——这是飞机通常飞行的高度，也是臭氧层浓度最高的地方。

这样看来，想要“穷千里目”，古人们只能想想了，而我们则可以坐上飞机，一饱眼福。当然了，如果实际去观测就会发现，云层的遮挡和能见度的极限，是阻碍我们看得更远的最大障碍。不过要是能站在地球之外，情况又会变的不一样。下图就是意大利人 2011 年 9 月 10 日利用高空气球飞升到接近 4 万米高空拍到的画面，此时的地平线已然是一条明显的弧线，俯瞰这个星球，风景当真很是不错。顺带一提，在完成了这个光荣使命后，这个气球也英勇就义，化作了碎片。

而如果你的目标更远大——想要看到半个地球的话，那还是趁早打消了这个念头吧。因为只有在无穷远点，才能够看到完整的半个地球。而很显然，无穷远点实际并不存在。

弯弯的地面弯弯的桥

地球是圆的，大地是弯的，在地面上的建筑物自然也都是弯曲的。一般的高楼大厦，因为底面积比较小不易察觉。但是对于跨度较大的建筑，例如大桥来说，这种弯曲则是非常明显的，也是需要在设计过程中考虑进去的。

金门大桥是美国旧金山一座非常有名的大桥，它的南端连接旧金山，而北端则连接着加州的马林县。这座桥有两个桥墩，整个桥的结构如下图所示：

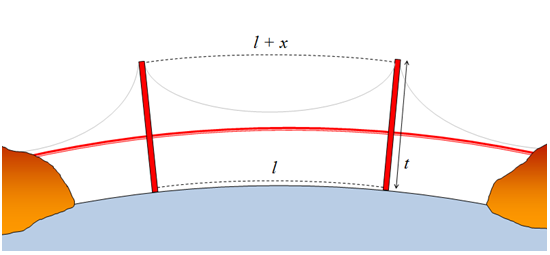
图中 t 为桥墩的高度，l 为两个桥墩在地面高度上的跨度。因为地面是弯曲的，所以对于这座大桥来说，两个桥墩所在的直线事实上并不平行。如果我们将这两个桥墩一直延伸到地心，可以得到下面这张图：

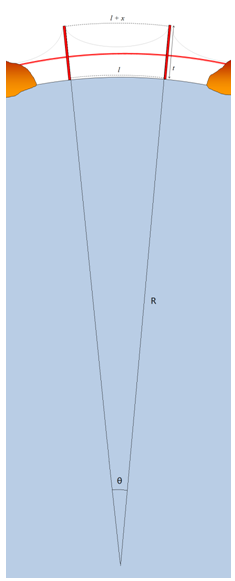
在这张图里，两个桥墩的延长线会交于地心，产生θ的夹角。图上有两个扇形，我们根据这两个扇形可以得到两个弧长公式：

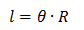
以及

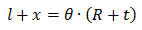
整理可得：

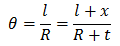
将 t=230m，l=1280m 以及 R=6371km 代入，很容易算出：

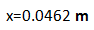
也就是说，金门大桥两个桥墩的上端间距比下端间距要大了 4.62 厘米，这正是地球圆大地弯导致的。

---

参考资料： Consequences of a living on a sphere