
(Ent/编译)我们都遇到过这种情况。你抓起一块披萨,正要一口吞掉的时候,披萨一下子软了,从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高,无法支持整片的重量。也许下次应该少加点儿料?不用,无需绝望。
如果你是个吃披萨多年的老手,那你应该知道怎么对付这样的场景:只需把披萨弯成U形即可。(手头没有披萨?拿一张纸试验一下就好。)
 一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
这个披萨小窍门的背后,深藏着一项关于曲面的强力数学。这一数学发现如此绝妙,以至于它的发明人——数学天才卡尔·弗雷德里克·高斯(Carl Friedrich Gauss)——给它起了个拉丁文名叫Theorema Egregium,意思是“绝妙定理”。
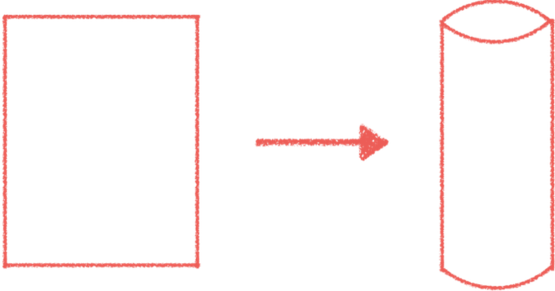
拿一张纸,卷成圆柱形纸筒。你可能觉得显而易见,纸本来是平的,卷成筒就弯了,对吧?可是高斯不这么想。他想给纸的弯曲程度(“曲率”)下一个定义,让它不因你人工施加的弯曲而改变。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia
如果你放大去看一只生活在纸筒上的蚂蚁,这只蚂蚁可以走很多条不同的路线。它可以沿着弯曲道路横着走下去,画出一个圆;也可以沿着平坦路线竖着走,走出一条直线。或者它可以把两种方式组合起来,走一条螺旋。
高斯的天才在于,他想到把所有这些路线都纳入曲率定义里面。办法是这样的:从任何一点出发,找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的,凹的路线曲率是负的,直的路线曲率是0。你得到的数字,就是那个点上的高斯曲率。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia
举几个例子吧。对于纸筒上的蚂蚁来说,最极端的两条路,一条是横着画圆,另一条就是竖着画直线。但是因为直线具有0曲率,所以乘起来总是得到0。照数学家的说法,纸筒是平的——它的高斯曲率就是0。这正是因为你能用平整的纸张卷出一个纸筒。
相反,如果蚂蚁活在一个球上,那么它就无法找到平坦的路线,每一条道路都会有一定程度的向外凸出,所以高斯曲率一定是个正的数。所以,球是弯的,而筒是平的。你可以把一张纸卷成一个筒,却永远不能卷成一个球。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia
高斯的绝妙定理就是:生活在曲面上的蚂蚁,根本不需要离开它就能知道曲面的曲率。只要测量一下距离,计算一下就行。顺便说,这也是为什么我们没有离开宇宙却能测量出我们的宇宙是不是平的(根据目前的观测来看,它是)。
但这个定理还有一个绝妙的结果:你可以随意弯曲一个曲面,只要你不拉长、压缩或者撕裂它,高斯曲率一定不会变。因为单纯弯曲不改变其上的距离,所以不管怎么弯,上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象,但是这推论有十分紧贴现实的结果。把一个橘子切成两半,吃掉里面的东西,然后把剩下半个橘子皮放在地上,踩吧。皮永远不可能被踩扁成一个完整的圆。相反,它一定会裂开。这是因为球面和平面拥有不同的高斯曲率,所以不扭曲、不撕裂,是不可能把球面压平的。有没有试过给人寄篮球当礼物?包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸,它总会留下一点点“平”的痕迹,所以最后只能得到皱皱巴巴一团糟。
 桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
这个定理的另一个推论是,平面纸上永远不可能画出准确的地图。很多常见世界地图投影方式能精确地保留角度,但是在面积上就有严重误差。数学博物馆的推特指出,服装设计师也面临类似挑战——他们在平面上设计花样,却要符合弯曲的人体。
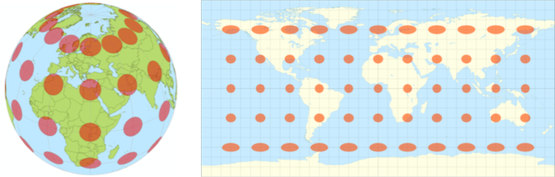 每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
那这一切和披萨饼有什么关系呀?是这样的:你拿起披萨之前,它是平的(数学上说,它的高斯曲率为0)。高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。当这片披萨塌下去的时候,平的方向(红色箭头)是朝侧面的,这对吃掉它可没有什么帮助。但是如果你抢在它塌下去之前,先把披萨侧着捏弯,就迫使另一个方向只能保持平整——也就是对着你嘴巴的方向。还真是绝妙的定理呀。
 没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
在一个方向上弯曲,来迫使它在另一个方向上保持平直。一旦你理解了这个点子,你就会到处都看到它。仔细看看一片草叶。它通常都是沿着中央叶脉弯曲的,这能帮助它维持笔直,不会软塌下去。工程师经常用弯曲来强化结构承载力。在马德里扎祖拉体育场,西班牙结构工程师埃杜拉多·托罗亚(Eduardo Torroja)设计了一套创新的混凝土屋顶,从边缘一直伸到看台上方,遮蔽了大片区域,而厚度只有几厘米。这其实就是披萨技巧。
 弯曲的草叶。图片来源:Dudley Carr / Flickr
弯曲的草叶。图片来源:Dudley Carr / Flickr
 西班牙扎祖拉体育场。图片来源:Ximo Michavila
西班牙扎祖拉体育场。图片来源:Ximo Michavila
弯曲带来力量。想想看:你能站在一个空易拉罐上,它能轻松承载你的体重;可是易拉罐外壁的厚度差不多和纸一样薄。它的秘密就是它的弯曲。如果有人趁你站在上面的时候拿笔戳一下易拉罐,就能戏剧化地展现这一点——只需一个小凹坑,它就会在你脚下轰然崩塌。
 纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
但最日常的例子可能是无处不在的波形建材。世界上简直没有比纸板箱更无聊的东西,但是撕开一个这样的箱子,你会看到箱壁里一条熟悉的波浪曲线。这些皱褶在里面可不是为了好看,它们是一种天才的结构方式:让材料又薄又轻,又能坚硬到足以承担可观的重压。
 很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
波形金属板使用的也是同样的原理。这些不起眼的建材是纯实用性的体现,它们的形态和其功能完美契合;它们的高强度和相对低廉造价使其成为了整个现代世界的背景。
今天,我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时,许多人把波形建材看成是奇迹材料。1829年,亨利·帕尔默(Henry Palmer)获得了波形建材的专利,他是一个英国工程师,负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起,但是听听当时的一家建筑学杂志是怎么描述它的吧:
不久前路过伦敦码头时,我们十分满意地发现,帕尔默先生新发明的屋顶已经得到了实际应用。……任何一个目光敏锐的人,路过的时候都不可能不被它的优雅和简洁所打动(虽然它只是个棚屋);而只要稍加思索,他们就会相信这一建筑的效率之高、经济之节约。我们认为,这是自亚当诞生以来,人类之手所建造的最轻又最结实(以其重量而言)的屋顶。若我们仔细观察(我们为了这一目的而爬过了各式各样的粘稠松油罐),会发现这一屋顶的总厚度绝对没有超过十分之一英寸!
这年头的建筑学杂志真是大不如前了啊。
虽然波形建材和易拉罐的强度可以很高,但有个办法让这些材料变得更强。想自己找到这个办法?去冰箱拿个鸡蛋出来。放在掌心,整只手握住鸡蛋,挤吧。(尝试这个的时候记得别戴戒指。)你会为它的强度而惊讶的。我就没法把鸡蛋握坏,哪怕用尽全力也没戏。(真的,谁试谁知道。)
 请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
鸡蛋为什么这么强?易拉罐和波形金属板在一个方向上是弯的,另一个还是平的。这一弯曲让它们拥有了一定强度,但它们还是有可能被压成本来的平板。
相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度。
 图片来源:Owen Cliffe / Wikimedia
图片来源:Owen Cliffe / Wikimedia
核电站冷却塔的象征性形状也在两个方向上利用了弯曲。这个形状叫做双曲面,能让所需的材料最少。正常的烟囱很像巨大易拉罐——结实是结实,但是很容易弯。双曲面形状的烟囱靠双向弯曲来解决这个问题,这样的弯曲方式能把形状“锁死”在空间中,提供额外的强度。
另一种得益于弯曲的形状是品客“薯片”,照数学家的说法,这是个双曲抛物面(hyperbolic paraboloid,舌头打结了没?)。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia
自然界运用这一形状的招数堪称脑洞大开。濑尿虾有一项臭名昭著的本领——动物界里最快的拳击手,它的一拳打出去的力道足以把着力点上的水蒸发掉,创造出冲击波和闪光。要想使出这死亡一击,濑尿虾使用了双曲抛物面形状的“弹簧”。平时它把弹簧压缩起来储存巨大的能量,然后一招之内释放出来。
西班牙-墨西哥建筑师菲利克斯·坎德拉(Félix Candela)很懂薯片形状的力量。坎德拉是托罗亚的学生,他的建筑将双曲抛物面带到了新的高度(字面意思)。当你听到“混凝土”这个词的时候,恐怕只会想到无聊透顶的方块建筑,但坎德拉却利用双曲抛物面盖起了巨大的建筑,使用的混凝土薄到不可思议。身为这一材料的真正大师,他既是极富创新的建筑者,也是结构艺术家。
 图片来源:Ciudad de las Artes y las Ciencias / Flickr
图片来源:Ciudad de las Artes y las Ciencias / Flickr
所以为什么薯片形状强度如此之高?这和它平衡张力与压力的方式有关。一切建筑都要支撑重量,最终将这些重量传递到地面上。这一传递可以靠两种不同方式完成:其一是压缩,拱顶就是纯靠压力而实现的例子;另一个就是拉伸,把一根锁链拎起来,它的每一环就都处于拉伸状态、受到张力。双曲抛物面结合了两种方式的优点。凹下去的U型部分处于拉伸状态,而凸起来的拱顶部分则是压缩,高斯绝妙定理则保证了任何一个地方的受力都会传递到四周——因为这是一个高斯曲率非零的曲面。只要你试图改变它的形状,就必须得连带压缩或者拉伸一整片区域才能让结果遵从高斯的律令;像纸张那样只弯曲一条线而不影响其他部分是不可能的。通过这样的双重弯曲,这一形状实现了张力和压力之间的精妙平衡,让它以很小的厚度就能实现惊人的强度。
通过弯曲来产生强度,这个想法塑造了我们所见的当代世界,而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候,记得朝周围看看,欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。(编辑:Calo)
参考资料
- Reid, Esmond. Understanding buildings: a multidisciplinary approach. MIT Press, 1984.
- Mornement, Adam, and Simon Holloway. Corrugated iron: building on the frontier. WW Norton & Company, 2007.
- Garlock, Maria E. Moreyra, David P. Billington, and Noah Burger. Félix Candela: engineer, builder, structural artist. Princeton University Art Museum, 2008.
