在《疑犯追踪》S02E11里,“宅总”哈罗德·芬奇说了这样一段话:

“π,圆周长与其直径之比,这是开始。后面一直有,无穷无尽。永不重复。就是说在这串数字中,包含每种可能的组合。你的生日,储物柜密码,你的社保号码,都在其中某处。如果把这些数字转换为字母,就能得到所有的单词,无数种组合。你婴儿时发出的第一个音节,你心上人的名字,你一辈子从始至终的故事,我们做过或说过的每件事,宇宙中所有无限的可能,都在这个简单的圆中。用这些信息做什么,它有什么用,取决于你们。”
很多观众看到这一段之后十分感动,还有人感慨:为什么我们的数学老师没有这么教我们呢?
之所以我们的老师不讲,是因为这段话在数学上是不对的。
无理
宅总的前两句话正确地描述了π的一个属性:无穷无尽且永不重复——换句话说,π是个“无限不循环小数”,也就是“无理数”。
但是,一个无理数并不一定能包含“每种可能的数字组合”。
举个简单的反例:0.909009000900009000009……
(除非特别声明,所有数字都是10进制的,下同。)
这个数的特点是,两个“9”之间的距离会越来越长,每次多一个0,直到无限。它是无穷无尽的,也是不循环的,因此是无理的;但别说“每种可能的数字组合”了,它连0到9这十个数字都凑不齐呢!
合取
包含所有数字组合的数,叫做“合取数”。无理数并不都是合取数。
一个典型的合取数是这样的:0.10200300040000500000600……000110000000000012000……
在越来越长的0串中间,夹杂着从1开始的所有自然数,直到无限。既然包含了所有自然数,当然也就包含了所有的数字组合。
正规
但是写这么多0,多费纸费电啊。如果把这些零去掉呢?
得到的数就是这样:0.123456789101112131415……
这个数不但是合取的,还是“正规”的——从0到9的每一个数字,出现的频率都趋向于一样的值。
随机
如果我们再进一步,连生成规律都不要了,而是用某种真随机生成器(比如哥本哈根解释下的量子随机性)造出一个每位都随机的数,那么它当然就是“随机”的了——不光每一个数字的长期频率趋于一致,任何位置出现的概率也都一样。
那pi是什么?
非常遗憾的是,目前为止我们只证明了pi是个无理数。pi是合取(包含所有可能)的吗?是正规(所有数字出现频率趋于一致)的吗?是随机(每一位上的数字都随机)的吗?
答案是:全都不知道。
我们很容易构造出一个合取数或者正规数,甚至能证明“几乎所有”实数都是合取而且正规的,但是随便拿一个具体的数字,要想判断它是否合取、是否正规,却极其困难。我们甚至都不知道pi里面是不是有无限个数字2。至于随机?别跟我提什么随机。
合取数和正规数有另一个有趣的性质:和进制有关。有个常数叫斯通汉姆数(Stoneham number),在二进制、四进制、八进制……下已经证明全都是正规的了,可是在六进制下却能证明它不是正规的。如果一个数在任何进制下都正规,可以称之为“绝对正规”。不幸的是,pi在任何进制下都没能证明正规——离得最近的是2,有论文证明,假如某个猜想是对的,那么pi就是二进制正规;但那个猜想本身也只是“很可能正确”,还没有得到严格证明。
当然,我们都已经计算出pi的几百亿位了,可以看看它们的分布来猜规律;也可以通过一些其他数学方法拐弯抹角地试图推断。从已知事实来看,pi和正规性吻合得非常之好,换做任何别的人文、社科、自然科学,都可以当做定论来用了,因此几乎所有人都“觉得”它该是正规的。可惜,这是数学,数学是靠证明说话的,只要拿不出证明,数学家就不能安心睡好觉。
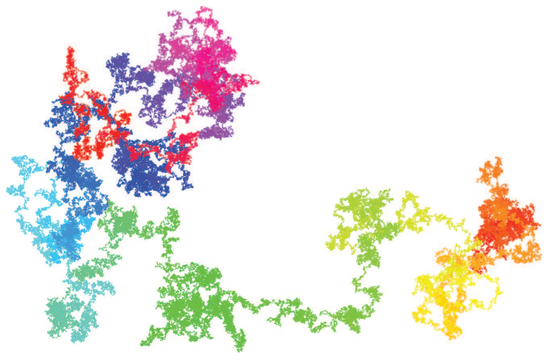 平面上的一个随机行走路线,每一步随机选择上下左右四个方向之一。本组行走路线图片来自David H. Bailey and Jonathan Borwein,下同。
平面上的一个随机行走路线,每一步随机选择上下左右四个方向之一。本组行走路线图片来自David H. Bailey and Jonathan Borwein,下同。
 用四进制pi前1000亿位生成的行走路线,0123分别对应上下左右。看起来和随机的很像。但只是看起来。
用四进制pi前1000亿位生成的行走路线,0123分别对应上下左右。看起来和随机的很像。但只是看起来。
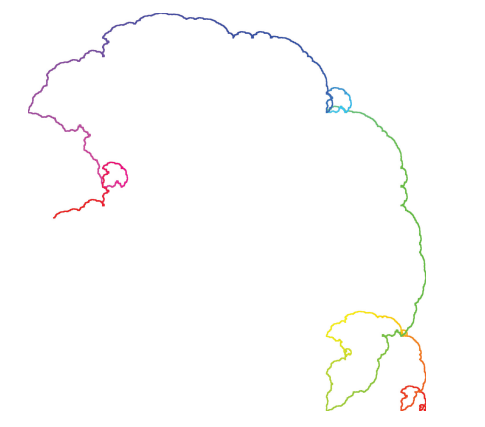 用四进制詹帕诺尼常数(Champernowne's number)生成的行走路线。这个常数是正规的,但显然一点儿都不随机。
用四进制詹帕诺尼常数(Champernowne's number)生成的行走路线。这个常数是正规的,但显然一点儿都不随机。
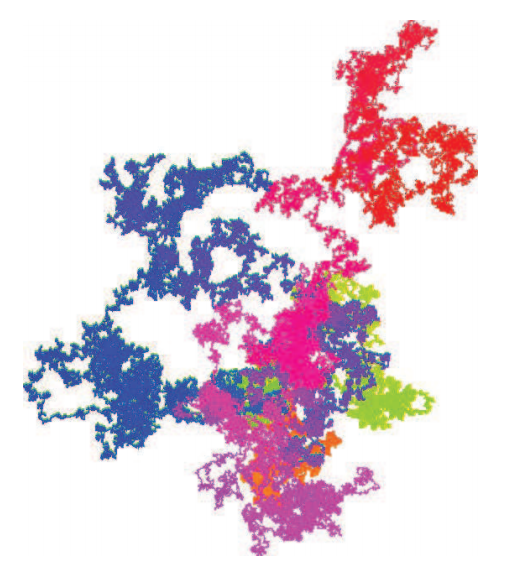 四进制斯通汉姆数生成的行走路线。它是正规的,看起来也很随机。
四进制斯通汉姆数生成的行走路线。它是正规的,看起来也很随机。
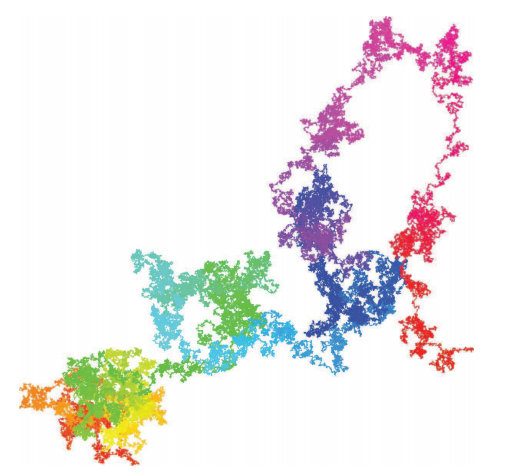 三进制斯通汉姆数生成的行走路线。我们不知道它是否正规,但至少看起来和随机很像。
三进制斯通汉姆数生成的行走路线。我们不知道它是否正规,但至少看起来和随机很像。
 六进制斯通汉姆数生成的行走路线。它不正规,所以……也完全不随机。就是这么一条儿。
六进制斯通汉姆数生成的行走路线。它不正规,所以……也完全不随机。就是这么一条儿。
为什么要在乎这些细节呢?
这篇文章不是为了批评《疑犯追踪》这部剧,事实上看到这一幕的时候我还非常高兴:影视剧里到处都是坏掉的理化生,而坏掉的人文社科干脆就是某些作品的主干——但现在终于出现了(哪怕是坏掉的)数学了!数学至少有了存在感!
但是这文章又必须要写,因为编剧在写这个段子的时候违反了基本的数学精神。其一,数学靠证明说话,哪怕pi距离“包含所有可能序列”离得再近,哪怕每一个人试过的每一个数字序列都能在它里面找到,在得到证明之前你也不能这么说;其二,数学是一个严密的逻辑体系,就算pi真的包含了所有可能性,你也不能说“因为它是无理数所以它是合取数”,这个推论本身的逻辑是错的。哪怕结果蒙对了,也不能为此放过错误的过程,否则整个数学体系就无法存在。
目前看来,pi“应该”是正规和合取的。如果让我打赌,我当然押“包含所有序列”一边;如果我在现实生活中用到了pi,我也会把它当做合取数和正规数那样用。甚至可以说,我“相信”pi是正规的:如果有人告诉我它不正规,我第一反应肯定是不接受;如果计算发现pi从第一万亿位开始变成了9090090009……,我没准都会开始怀疑宇宙的真实性——但是,只要没有出现证明,我就不能言之凿凿对你说:“pi里面包含了所有可能的数字组合”,更不能用似是而非的推论来支持这个说法。经验、审美甚至信仰,在数学里,都敌不过薄薄的一纸证明。
其实死理性派也有情怀,只不过往往用在了奇怪的地方。(编辑:球藻怪)
P.S. 下面是一些和pi相关的网页:
有个工具能在pi的前2亿位里搜索任何一个数。范围里搜到任一八位数生日的概率是86%。
WolframAlpha整理了一些关于pi的有(wu)趣(liao)小知识。
这个网页上列举了pi的前100万位。
基于pi“很可能有”的合取性,有人半开玩笑地设计了一套文件系统“πfs”,你的所有的数据都(很可能)存在pi的某一个地方,只要找到那个地方就好了。
参考文献
- David H. Bailey and Jonathan Borwein. Pi Day Is Upon Us Again and We Still Do Not Know if Pi Is Normal. American Mathematical Monthly, Mar 2014
