如果你问苹果手机上的Siri,“零除以零等于多少”,它会显示:
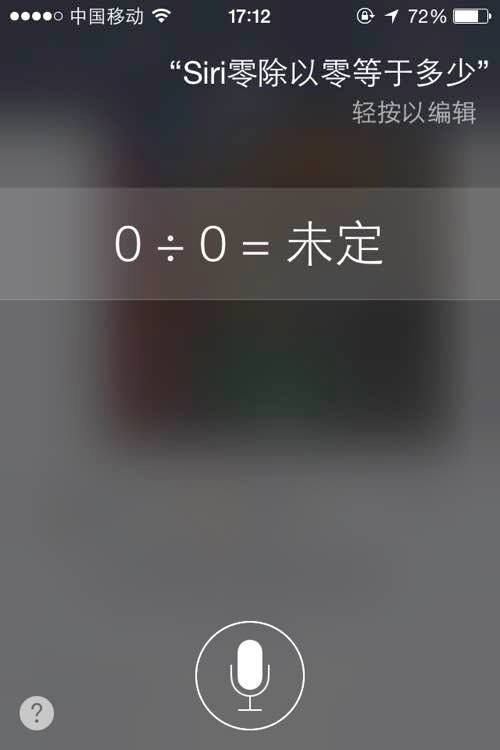
但是,英文版的Siri还会用语音说这一段话:
“假如你有0块饼干,要分给0个朋友,每个人能分到几块?你看,这个问题没有任何意义吧?甜饼怪会难过,因为没有饼干吃,而你也会难过,因为你一个朋友都没有。”
(中文版也会,但言辞就没那么伤人了……)

抛开这个伤人的回答不论(有朋友谁特么会跟你聊天啊喂!),除以零确实是个困扰很多人的问题。十除以二等于五,六除以三等于二,一除以零是多少?小学数学就会告诉你,答案是不能除。但是为什么?零也是个数字,它到底哪里特殊了?
小学篇
小学算术里,这个问题很简单。那时我们把除法定义成“把一个东西分成几份”,分成一二三四五六七份都很容易想象,但是你要怎么把10个饼干分给0个人呢?想象不出来嘛!所以不能除。
敏锐的同学可能会想到,要是0个饼干分给0个人的话,本来无一物,好像就没关系了。但既然无物也无人,每个人分得多少都是可能的呀,根本无法给出一个单一确定的数值。
这结论没错,但这都是凭直觉而得到的东西。你想象不出来,不一定意味着它没有。远古时代的数学是建立在直觉上的,买菜是够用了,但要进一步发展,就必须要有定义和证明——所以,我们上了中学。
初中篇
现在我们开始接触最最基本的代数学——也就是解方程。我们发现,除法和乘法互为逆运算,所以问
1 / 0 = ?
就等于是解方程
0 * x = 1
好了,按照定义,0乘以任何数都是0,不可能等于1,所以满足x的数字不存在,所以不能除。
同样,如果问
0 / 0 = ?
就等于是解方程
0 * x = 0
同理,任何数字都可以满足x,所以也不能除——无法确定一个单一的答案。
高中篇
等到接触了基本的形式逻辑,我们又会发现另一种证明方式:反证法。
一堆真的表述,不能推出一个假的表述,所以如果我们用“能够正常地除以零”加上别的一堆真表述,最后推出假的来,那只能说明“除以零”这件事情不成立了。
所以,已知
0 * 1 = 0
0 * 2 = 0
推出 0 * 1 = 0 * 2
两边同时除以零,得到 ( 0 / 0 ) * 1 = ( 0 / 0 ) * 2
化简得到 1 = 2。这显然是错的啦。
那么,问题解决了吧!其实还没有。想想另一个问题:-1的平方根是多少?
你可能会说,-1不能开平方根,因为所有数的平方都是非负的。但是这说的是实数,我要是增加一个定义呢?定义i^2=-1,这就创造出了虚数,于是-1也能开平方根了。
那么,为何不能定义一个“新”的数,让 1 / 0 也等于它,并为这个数设立一套运算法则呢?这就得去大学里回答了。
大一篇
刚学微积分课程就会立刻接触到∞这个符号。咦,这不就是“无限”嘛。我们都学了极限的概念了,那么我令b趋向于0,然后把a/b的极限定义为无穷,不行吗?
这就立刻遇到一个问题,它的左极限和右极限不一样啊。b是从负的那头靠近0,还是正的那头?这一个是越来越负,一个是越来越正,碰不到一起去。这样的极限是没法定义的。
因此,微积分课程里会反复说,虽然用到了∞这个符号,但是这只是代表一个趋势,绝对不是一个真正的数,不可参与运算。
大二篇
那么吸取教训,我不用现成符号了,我直接定义 1 / 0 = w,w是个“无限大”的数,不碰什么极限,你总没话说了吧!
然而,定义不是说来就来的,你虽然可以随便定义东西,但定义完了如果和现有的其他系统矛盾,那就不能用,或者很不好用。
而我们面对w立刻就遇到了问题。首先,w要怎么放入基本的加减乘除体系里?1 + w等于多少?w - w等于多少?如果你造了一个数,却连加减乘除都不能做,那就不是很有用对吧。
比如直觉上,1 + w 应该等于 w,它都无限了嘛! 而 w - w 则等于0,自己减自己嘛!
但这样立刻会和加法里极其重要的“结合律”产生矛盾: 1 + ( w - w ) = 1 + 0 = 1,可是( 1 + w ) - w = w - w = 0。结合律是加法里非常基本的东西,为了一个w,连结合律都不要了,这成本有点大——不光是结合律本身,多少数学定理证明过程中不自觉都用了它,扔了它就都得重来,建立新体系。新体系不是不能建,但是费心费力又(暂时)无卵用,所以大家还是在老实用旧的——而旧的里面,为了保住结合律,就不能这么玩。
欢迎读者们发挥自己的想象力,尝试为 w 给出运算方式。但是你会发现,无论怎么规定w和别的数字之间的关系,只要你还坚持 1 / 0 = w,你就没法让它和你从小学习的基本数学不矛盾。还是那句话,你可以另立门户,在w的基础上建立起你的新数学,但它和大部分传统数学是不相容的,而且肯定会非常不好用,所以我们用了一个不能除以零的体系是非常合理的。
大三篇
你可能会提出反对:有那么多的定义方式,我都试过?要是没试过,我怎么知道不会某一天冒出来一个能够自洽的办法?
“新发现推翻旧结论”这种事情,在生物里可以有,化学里可以有,物理里可以有,唯独数学里没有。因为数学建立在逻辑上,个案有例外,逻辑没有例外。当然我们的数学还没有完成最终公理化,还要面对哥德尔的幽灵,但至少在这个例子里,如果w是一个真正的数,那它就违反了一些非常重要的公理,而这些公理的地位可是非常之深。
比如有一组基本的公理叫“皮亚诺公理”,其中有一条说,每一个确定的自然数都有一个确定的后继,后继也是自然数;另一条说,自然数b=c,当且仅当b的后继=c的后继。
那w是谁的后继呢——或者说,谁加上1能得到w呢?显然所有其他的数字都已经有了自己的后继,w在其中没有位置,没有任何其他的数加上1能成为w。那么就只能是1+w=w了,可那就直接和第二句话矛盾。而没有皮亚诺公理,整个自然数的体系都不能成立。
这里假定w是自然数。其他情况会略微复杂一些,但无论如何,类似的事情发生在w的各种定义里。如果你想把w当成一个数,那就没法和我们现有的实数兼容。所以我们在几乎所有场合下都只能宣布,不能除以0。
大四以上篇
既然我们之前说了个“几乎”,那就是有例外的——在个别奇葩场合下,可以。
比如有一个东西叫做“复无穷”,它是扩充复平面上的一个点,真的是有定义的一个点。在这个特殊的规则下你可以写下 1 / 0 = ∞ 这样一个表达式。这么做的原因就说来话长了,但它不是平常意义上的运算——比如你不能把0拿回来,不能写 1 = 0 * ∞。
另外,“无穷”二字在一些别的场合下是可以当成一个“东西”去对待的。比如当你衡量一个集合的大小的时候,它可以是无穷大的。但这就有很多种不同的无穷大了——自然数是无穷多的,有理数是无穷多的,实数也是无穷多的,可是奇数和偶数和正整数和负整数和自然数和有理数都一样多,而实数却比它们都多!同样是无穷,有的无穷比别的无穷更无穷。但这就是另一个话题了,打住。
总结篇
所以,当我们说不能除以零的时候,理由……竟然出乎意料地充足。有许多直觉在数学里被推翻了,但是这一条没有。我们有种种数学上的方式去证明它无法成立的原因,虽然也许听起来不如Siri的回答那么心暖(或者心寒),但这些理性的愉悦也是一种美丽,对吧?
(编辑:Ent)
