对于我来说，科研最本真的快乐，就是能够找出一条新的定律。
何其有幸，我梦想成真了。
快乐的费曼先生
费曼之所以被称为最具传奇色彩之一的物理学家，可能要归功于他的“路径积分”和与之伴生而来的“费曼图”。而一提起费曼最大的物理学贡献，大家也会不约而同的认为是“路径积分”。我也是这么认为的。
不过，费曼可能并不这么认为。他觉得自己在量子理论的“路径积分”上的基本贡献，主要是提供了一种新的计算方法。而他对自己在超流等研究工作上的评价是：仅仅是对已经发现的物理现象的解释。那么，费曼觉得自己的什么工作最重要呢？
他认为：是弱相互作用的“普适V-A理论” [1]。
费曼：我最喜欢的工作，是我自己找出的一条规律。图片来源：findagrave.com
这个工作由费曼和盖尔曼合作完成，并发表于1958年的美国《物理评论》。
费曼在完成弱相互作用的“普适V-A理论”之后，非常的沾沾自喜，他认为“这是我第一次发现一条新定律”。只有这一次，才真正满足了他从小要找出物理学的规律，揭示自然之谜的梦想 [1]。
费曼的梦想是实现了。那么我的梦想呢？
我的梦想：发现一条新的物理定律
我的梦想与费曼一样（很多人可能也一样）：“找出物理学的规律，揭示自然之谜。”要是能发现一条新的物理学定律，那我也一样会沾沾自喜一阵子。
但是，那可能吗？
物理学的梦是2001年开始的吧，到现在刚好15年了。我现在还清晰的记得2003年时听人说到“我们生活在一个物理学黄金时期早已过去的年代”。现代物理学基本上已经不可能再发现什么伟大定律。
现代物理学可能发现不了“伟大定律”，但我会尝试着找寻“小小定律”。图片来源：feministing.com
我想，既然伟大定律发现不了，那么发现一些小定律总可以吧。
后来被人告知，已知的定律实验都已经检验不完，谁有空管小定律啊？再过几年才发现，现实是残酷的，21世纪的理论物理学家已经远远的“超越”了时代，提出了各种理论，比如，弦论。理论物理学家也是绝对自信的一群家伙，他们很多人都相信自己的理论是正确的，而现实物理呢，在他们一些人的眼里不过只是调调参数的“私人玩具”而已。
所以呢？我放弃了变成“爱因斯坦”的梦想。我想：既然发现不了伟大定律，管不了小定律，那么就不妨尝试找找“小小定律”吧。
我和我的“小小定律”
什么是“小小定律”呢？在我的眼里，“小小定律”不像“超弦理论”那么伟大，后者希望去解释宇宙的全部；当然，“小小定律”也不像“小定律”那样，后者别人没有闲工夫管；“小小定律”只需要别人有兴趣来管一管，并且小小的满足一下揭示自然之谜的“成就感”就好。
结果像大多数的故事情节一样，我找到了一个我所珍爱的“小小定律”：超导-正常态临界转变温度Tc附近的“标度法则”。这个标度法则有什么用呢？很简单，它可以用来标示超导的临界转变温度Tc，并且能够用这个法则提升这个转变温度，让它在工业上能够实现。
所以，我的“小小定律”上个月发表在英国自然出版集团的期刊Scientific Reports上[2]，论文下载链接在这里。
“小小定律”不平凡
那么，我的“小小定律”有什么与众不同之处呢？要知道高温超导可是一个很难的问题啊。别人的可能很难，不过，我的却很简单，因为我讨厌复杂，喜欢简单。难道就一定要弄清微观机理才能制作高温超导吗？我不信。
20世纪的时候，著名的前苏联物理学家Landau和他的学生Ginzburg提出了一个描述低温超导的唯像模型，被称为Landau-Ginzburg模型，这个模型之所以被称为唯像模型，是因为它的微观机理不清，并且模型中的参数具体是什么也是未知的：
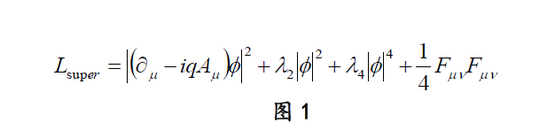
不过，后来另一位前苏联的物理学家Gorkov发现Landau-Ginzburg模型可以从著名的Bardeen-Cooper-Schrieffer(BCS)超导模型中被推导出来，并且由BCS模型推导而来的Landau-Ginzburg模型的系数可以被精确的固定下来 [3]：
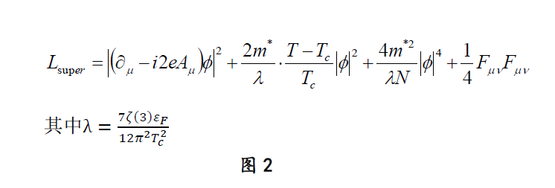
有意思的是，图2中的Landau-Ginzburg模型的系数中包含超导的临界转变温度Tc，这是否意味着如果在Landau-Ginzburg模型中再加上一项新的作用量，并且该作用量的系数x具有宏观物理意义，那么就可以通过处理“临界现象”的“重整化群”方法找到临界转变温度Tc与x的关系呢？
由于“x”具有宏观物理意义，那么操控这个“x”就有望提升临界转变温度Tc。
临界转变温度是指材料在降温到一定程度后，电阻变为零时的温度。超导还有一个表现：完全抗磁性。图片来源：news.livedoor.com
众所周知，高温超导是一个强关联系统，那么什么样的相互作用可以描述强关联系统呢？分数量子霍尔系统告诉我们，Chern-Simons规范场可以做到这一点。有意思的是，Chern-Simons规范场的系数具有宏观物理意义——霍尔电导率（非对角电导率）。所以，我就得到了我的高温超导模型：
我的高温超导模型用的是3维空间的Chern-Simons规范场，而不是2+1维时空的Chern-Simons规范场，后者描述分数量子霍尔系统。
之前的看不懂没关系，接下来的就比较容易理解了。
对我的高温超导模型实施重整化群方法，我还就真得到了一个标度法则：
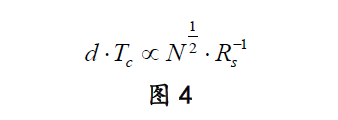
看，是否很简单呢？
我的超导标度法则将超导转变温度Tc、材料厚度d、材料的（薄膜）电阻Rs、材料正常态时的电子数密度N联系起来。只用调节后面三个参数d、Rs和N，就有望提升超导转变温度Tc。
“小小定律”正确吗？
首先，我看到2014年美国MIT一个实验组在Physical Review B发表了超导临界温度附近的一个标度法则 [4]：
结果，我笑了。这不是说明Tc和我之前提到的材料厚度d和材料的（薄膜）电阻Rs相关吗，指数也在误差范围内。
这两天，我又看到美国俄亥俄州立大学一个实验组以及美国布鲁克海文国家实验室分别于2007年在 Nature Physics 和2011年在 Nature 上发表了超导临界温度附近的一个标度法则[5-6]：
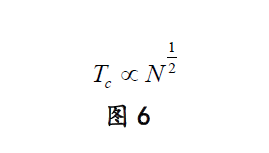
结果，我沾沾自喜了。这是证明了材料正常态时的电子数密度N和超导转变温度Tc的关系
到现在，我终于相信，我很可能发现了一个属于我的“小小定律”。
所以，我相信了，找出物理学的规律，揭示自然之谜，内心会是快乐的。
所以，我相信了费曼先生，因为他曾经也快乐过。
最后，希望大家都能找到内心的快乐。（编辑：Jerrusalem）
参考文献：
- 费曼著，《物理定律的本性》，湖南科学技术出版社，2012年9月，214页
- Yong Tao, Scaling Laws for Thin Films near the Superconducting-to-InsulatingTransition. Scientific Reports, DOI: 10.1038/srep23863 (2016).
- Gorkov, L. P. Microscopic derivation of the Ginzburg-Landau equations in thetheory of superconductivity. Soviet Phys. JETP 9, 1364–1367 (1959)
- Ivry, Y. et al. Universal scaling of the critical temperature for thin filmsnear the superconducting-to-insulating transition. Phys. Rev. B 90, 214515 (2014)
- Hetel, I. et al. Quantum critical behaviour in the superfluid density ofstrongly underdoped ultrathin copper oxide films. Nature physics 3, 700-702 (2007)
- Bollinger, A. T. et al. Superconductor–insulator transition in La2-xSrxCuO4 atthe pair quantum resistance. Nature 472,458-460 (2011)