能不能简单解释黎曼猜想是什么?其实可以。
但是话说在前面,越是简单的解释,丢失的信息就越多,所以解释得越简单,就越难接着解释为什么这个东西很重要。
用我能想到的最简单办法解释,是这样的:根据一个重要的数学公式,能画出很多很多个点,实际上有无穷多个这样的点。黎曼觉得,这些点有一部分排成一条横线,另一部分排成一条竖线,所有这些点都在这两条线上,没有一个漏网的。
这么一说是不是感觉没有什么了不起的样子?那就稍微扩展一点:
首先,有一个很重要的函数,叫黎曼泽塔函数。
这个函数是一个复函数,可以把它理解为有两个变量的函数,一个叫实部,一个叫虚部。写成熟悉的函数样子的话,那就是 y = f (实, 虚)。
这函数长得有点复杂,但可以先从简单情况看起:假如我们先不管虚部,强制让虚部=0,那就是一个很普通的函数 y = f’ (实) 了。这个函数长啥样呢?
【图1】是它的一部分。你会发现它有一个明显特点:当实部=-2、-4、-6、-8、-10……等等的时候,这个函数都和x轴相交。换言之,它的函数值在这些时候都是0.
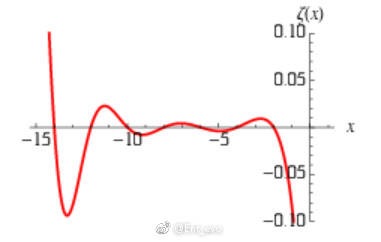 【图1】
【图1】
这就是我们想要的东西:让黎曼泽塔函数的函数值取0的点。
当然,这些点太显然了,很没意思,用数学家的话说就是这都是“平凡”的解。简单的原因是,我们刚才只考虑了虚部=0的情况。如果允许虚部随便取,那要怎样才能让函数值取0呢?
这就是黎曼的猜想了:为了让函数值取0,除了这些平凡解之外,剩下的所有解,不管虚部多大,实部都一定是1/2。
或者说,如果我们把所有的解画在坐标轴上,实部是横,虚部是纵,那么它们应该像【图2】这样,除了左边-2、-4、-6那一串,剩下右边的,全都在1/2的这条红线上。
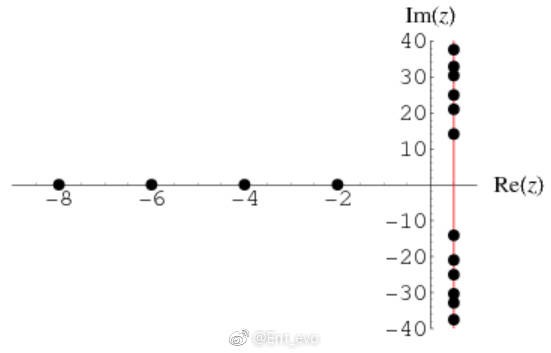 【图2】
【图2】
换句话说,“黎曼猜想指的是:对于黎曼泽塔函数,其非平凡零点的实数部分都是1/2。” 也可以表述成,“黎曼泽塔函数的零点要么是负偶数,要么是实部为1/2的复数。”
……凭什么啊?
不知道!但这就是黎曼的猜想,而且这个猜想如果成立的话,将会非常非常非常的好用。实际上,数学家们已经在假定它成立的情况下,从它推出了成百上千条定理,涉及到好多好多领域的数学。假如有一天突然发现黎曼其实猜错了,那大家就会很慌,有很多本来习以为常的东西都错了,就像大厦的地基突然塌陷;但大家也会很兴奋,因为这就意味着很多之前认为做不了的事情突然又可以做了。
但反过来如果终于有人能够彻底证明黎曼真的是对的,那……其实不会造成什么立即的动荡,因为大家一直都是假定它是对的,只不过终于所有人都能松一口气睡个安稳觉了。(必须指出,黎曼猜想并不能直接用来解决大质数分解问题,它的成立并不意味着我们的加密系统要立刻完蛋。)
不造成立刻动荡,不意味着证明不重要。为了这个定理大家已经花了一百五十多年,常规的办法都试过了都不太管用,所以如果有人真的证明了它,几乎肯定是找到了一条前无古人的新路线;而因为黎曼猜想的地位十分核心,所以这个路线几乎肯定能用来干好多别的厉害的事情,甚至开辟一整个新领域。上一次出现这种事情,是证明费马大定理。费马大定理本身其实没有特别特别重要,但是为了证明它而开发出的一系列数学工具改变了数学界的面貌;对于黎曼猜想,大家等的也是这样的场景。
但究竟能不能等到嘛……这次就看24号海德堡大会上Michael Atiyah爵士到底能讲出啥来了 _(:з」∠)_

以及,一个PS:
如果对黎曼泽塔函数取-1,就得到了那个著名的“公式”:1+2+3+4+……=-1/12。
但是,这不是加法!不是加法!不是加法!不是说自然数的和是-1/12!这是一个发散的级数,按照标准的加法,谈论它加起来是啥根本没意义。
这个公式最早是欧拉搞出来的。欧拉那个时代,大家没有搞明白微积分,做了很多乱来的事情,后来两百年才慢慢救回来。欧拉证明这个“公式”的做法,按照今天的标准,就是错的。没悬念。
但是后来的数学家发现,虽然欧拉的证明是错的,但是在有些特定的场合下,比如物理上的重整化或者数学的模形式,说“黎曼泽塔函数在-1处的值为-1/12” (或者,ζ(-1)=-1/12),这样做居然很有用……
怎么说呢,牛人运气好,欧拉蒙对了(虽然他几乎肯定不知道自己蒙对了啥)。
但总而言之,在这个问题上数学家们费了很大的劲,重新定义了加法(真的),用很麻烦的严格办法让ζ(-1)=-1/12这个事情能够成立。但是今天的数学家已经没有人会把它写成“1+2+3+4+……=-1/12”了。这样做一是没有必要,二是引起误解:这里的加是所谓拉马努金求和,根本就不是我们日常熟悉的那种加法。
所以再重复一遍:所有自然数加起来不是-1/12,而是一个没有意义的东西,就像你算1÷0得到的是没有意义的东西一样。
今天油管上有很多视频说证明1+2+3+4+……=-1/12,这些视频99.99%都是错误的证明,都是乱搞,有的和欧拉一样蠢,大部分比欧拉还蠢得多(咦这话说出来好像不是贬义)。还有好几个类似的,比如1-1+1-1+1……=1/2,也是差不多的现象,错误的证明满天飞;你可以给它一个严谨的证明,但那个证明会很难,而且使用的也不再是我们熟悉的加法减法。
