搜索的时候，我们肯定希望最重要的网页排在最前面。可是，怎样判断一个网页的重要性？

互联网的网页多如猫毛，一个个人工去判断，肯定是不可能的。懒惰如你我，这么麻烦的事情，还是让网页自己来决定吧。这样，对我们而言，一个很自然的想法是：一个网页获得链接越多，可信度就越高，那么它的排名就越高。

这个看似简单的想法，正是谷歌PageRank网页排名算法的核心思想。

图：Pixabay

不过，算法实际上要复杂的多。比如，你想呀，把每个网页获得的链接从多到少排名一下可以吗？好像也不行，光是想想庞大的网络水军就知道，这样排名的注水量一定能淹了龙王庙。这很容易作弊不说，也不能反映不同网页内容和领域的差异。

假如，你是学校的招生老师，看推荐信，是看谁的信多谁厉害吗？当然不是，还要看写信的人是谁。同样的道理，我们应该看一下链过去的网页到底有多厉害。如果一个网页被很多其他网页所链接，由于有的网页重要，而有的网页很水，我们当然要对来自不同网页的链接区别对待。因而，在判断一个网页的重要性时，对那些重要网页的链接应该给予大的权重，而权重又取决于它们的重要程度——被链接的次数……

这样，问题就来了。和单向的推荐信不同，所有的网页都是连在一起的，你链我、我链她、她链他，他链我，构成了一个死循环。而你评估必须要有一个起点，但是，用任何网页作为起点都不公平，怎么办？

PageRank的解决办法是：先同时把所有网站作为起点，也就是先假定所有的网页一样重要、排名相同。然后，进行迭代。

同时起点又该怎么做？这时候，就是线性代数非出场不可的时候了。

1996年，谷歌的创始人拉里·佩奇（Larry Page）和谢尔盖·布林（Sergey Brin）在斯坦福大学开发出PageRank。“Page”一语双关，既有网页的意思，也是佩奇的名字。当时，佩奇和布林把整个互联网当做一个整体来看待，他们认为“整个互联网就像一张大的图，每个网站就像一个节点，而每个网页的链接就像一个弧”^【1】。于是，佩奇就想用一个图或者线性代数的矩阵来描述互联网。而布林把无从下手的网页相连问题变成了一个二维矩阵相乘的问题，并通过迭代，算出了网页排名。

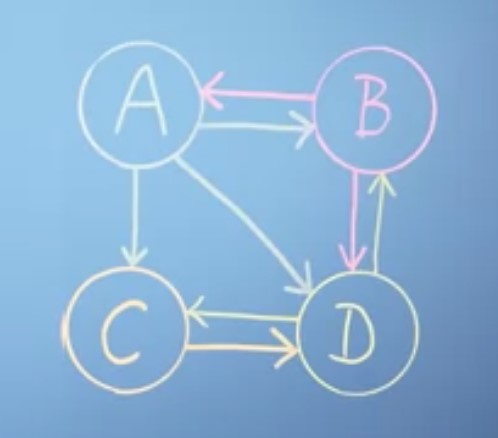图1，四个网页之间的链接情况

布林先假定所有网页的排名是一样的：一共n个网页的话，那每个网页的最初排名都是1/n。假设一共4个网页（见图1），那每个网页的初始排名都是1/4，当我们用一个向量r来保存所有网页的排名时，r的初始值就如下所示：

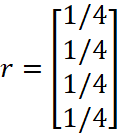r的初始值，即所有网页的初始网页排名

然后，我们把一个网页的链接情况看作是一个向量，那么，根据图1，网页A的链接情况。以此类推，， ，。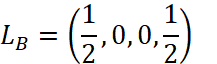

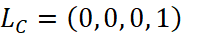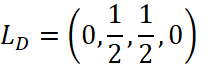这样，我们就能把所有网页之间的链接情况用一个矩阵L表示：

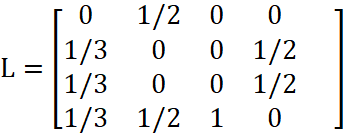列：指向外部的链接数，行：指向自己的链接数，例如，第一列表示从A指出的链接数，第一行表示箭头指向A的链接数。

我们已经知道，一个网页的重要程度，要看它被多少网页所链接；同时，对于不同的链接网页，根据它们的网页排名，我们给予不同的权重。所以，网页A的排名应该等于所有指向网页A的其他网页的权重之和。而我们现在既知道所有网页的链接数——矩阵L，也知道所有网页的排名——向量r，那么，就可以算出一个网页的排名，比如网页A的排名：

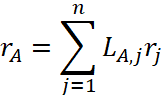j表示第几个网页

接着，就开始迭代。当所有网页的最初排名都一样的时候，我们可以算出每个网页的第一次迭代排名。网页A、B、C、D的第一次迭代排名计算如下：

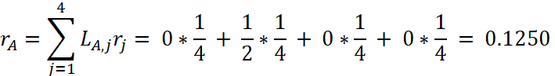
网页BCD的第一次迭代排名依次为0.2083、 0.2083、 0.4583。

有了第一次迭代排名，我们又能算出第二次迭代排名……最终，排名r会收敛，不再变化。一般只要10次左右的迭代基本上就收敛了。而且，这种算法不需要任何人工干预。如下图，经过多次迭代，红框内的数值，就是这四个网页的最终排名：D排最前面，中间是B和C，排在最后的是A。

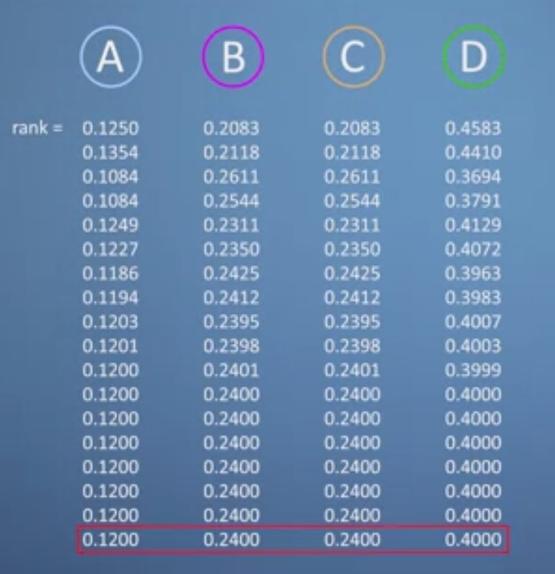图：coursera.org- Imperial College London, Mathematics for Machine Learning: Linear Algebra

迭代计算的结果会收敛到网页排名的真实值吗？打比方的话，网页之间的链接关系，有点类似动物之间的食物链关系。而网页排名结果通过多次迭代、最终收敛，就有些类似于常见的兔子数量问题，在一个自然的生态环境里，不管兔子最开始的数量是多少，最终它们的数量都会达到一个稳定的值。关于网页排名计算的迭代收敛，佩奇和布林从理论上证明了不论初始值如何选取，这种算法都能保证网页排名的估计值能收敛到排名的真实值^【1】。

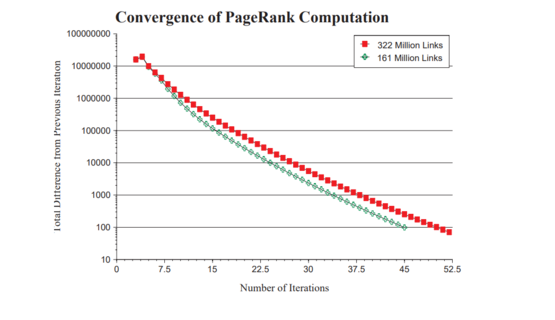随着迭代次数的增加，与上一次迭代结果的总差异在变小

简言之，网页排名的的计算主要是矩阵相乘。但是，在实际运用中，这些运算其实非常复杂。另外，实际的网页数量多得惊人，巨大的矩阵相乘需要的计算量也就无法估计，而这也难不过科技大牛们，佩奇和布林又利用稀疏矩阵计算的技巧解决了庞大计算量这一问题。但是现在，对一个网页重要性的衡量是全方位的，除了要看PageRank，还要看别的数据，比如网页的内容权威性……

谷歌PageRank网页排名算法，让谷歌搜索引擎从同时代的搜索引擎中脱颖而出，也让两位创始人成为了亿万富翁。换句话说，线性代数不仅能拿来修学分，还有可能让你成为富翁。

现在，妈妈再也不用担心我不知道线性代数能干啥使了……（编辑：Ent）

参考资料：

1. 吴军. 数学之美[M]. 人民邮电出版社, 2012.
2. https://www.coursera.org/lecture/linear-algebra-machine-learning/introduction-to-pagerank-hExUC
3. Page L, Brin S, Motwani R, et al. The PageRank citation ranking: Bringing order to the web[R]. Stanford InfoLab, 1999.
4. Brin S, Page L. The anatomy of a large-scale hypertextual web search engine[J]. Computer networks and ISDN systems, 1998, 30(1-7): 107-117.
5. https://en.wikipedia.org/wiki/PageRank

题图来源： Pixabay