e是增长极限

到底什么是e？简单说来，e就是 增长的极限 。

下面这个例子就是对e直观含义的极好诠释:

某种类的一群单细胞生物每24小时全部分裂一次。在不考虑死亡与变异等情况下，那么很显然，这群单细胞生物的总数量每天都会增加一倍。据此我们可以写出它的增量公式：

growth= 2 ^x x表示天数

这个式子可以改写成如下的样子：

growth= (1+100%) ^x 其中，1表示原有数量，100%表示单位时间内（24小时）的增长率。

根据细胞生物学，每过12个小时，也就是分裂进行到一半的时候，平均会新产生一半原数量的新细胞，新产生的细胞在之后的12小时内已经在分裂了。

因此一天24个小时可以分成两个阶段，每一个阶段的细胞数量都在前一个阶段的基础上增长50%：

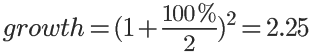
即在一个单位时间内，这些细胞的数量一共可以增至为原数量的2.25倍。

倘若这种细胞每过8小时就可以产生平均1/3的新细胞，新生细胞立即具备独立分裂的能力，那就可以将1天分成3个阶段，在一天内时间细胞的总数会增至为：

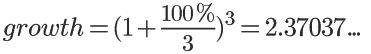
即最后细胞数扩大为2.37倍。

实际上，这种分裂现象是不间断、连续的，每分每秒产生的新细胞，都会立即和母体一样继续分裂，一个单位时间(24小时)最多可以得到多少个细胞呢？答案是：

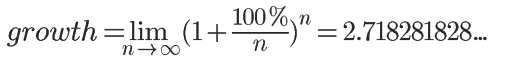
当增长率为100%保持不变时，在单位时间内细胞种群最多只能扩大2.71828倍。 数学家把这个数就称为e，它的含义是单位时间内，持续的翻倍增长所能达到的极限值 。

这个值是自然增长的极限，是“自然律”的精髓所在，因此以e为底的对数，就叫做自然对数。

你不会自成“大款”——到e为止

有了这个值以后，计算银行的复利就非常容易。

假定有一家银行，每年的复利是100%，请问存入100元，一年后可以拿多少钱？

答案是：

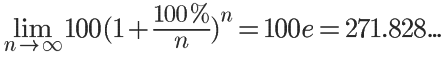
但是事实上，存储利息没有这么高，如果复利率只有5%，那么100元存一年可以拿到多少钱呢：

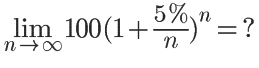
我们知道，在100%利息率的情况下，n=1000时，下式的值非常接近e：

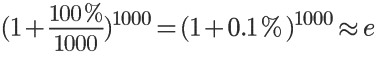
为了便于思考，取n等于50：

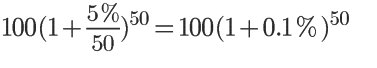
当利息率是5%时，存款增长率就相当于e的20分之一次方：

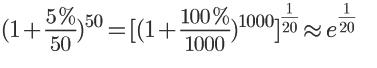
1/20正好等于5%，所以我们可以把上式改写成：

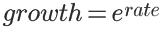
rate表示利率。

再考虑时间因素，如果存款年限t年，那么存款最终增长率为：

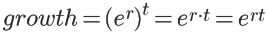
这说明e可以用于任何连续不断的复合式增长率的计算，而上式也是这个增长率的通用计算公式。

带着这个结论再回到上面的例子。如果银行的利息率是5%的复利，求解100元存款翻倍需要多少时间就等价于解下面的方程：

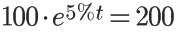
计算结果得13.86年：

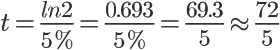
可以看到：用72除以增长率就是翻倍的大致时间。这正是经济学上著名的72法则。

编者按：e是“指数”（exponential）的首字母，也是欧拉名字的首字母。和圆周率π及虚数单位i一样，e是最重要的数学常数之一。第一次把e看成常数的是雅各布•伯努利，他开始尝试计算lim（1+1/n） ⁿ 的值，1727年欧拉首次用小写字母“e”表示这常数，此后遂成标准。

本文来源： 阮一峰的网络日志

原文出处： http://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e/