统计一下世界上237个国家的人口数量,你觉得其中以1开头的数会占多大比例,而以9开头的数又占多大比例呢?如果你的回答是都为1/9,恭喜你你是正常人,但是事实却不是如此:以1开头的数惊人的占到了27%,而以9开头的数却只占5%。下图可以很形象的展示出在各国人口数量问题上,以各个数字开头的数占了多大的比例(图片来自维基百科)。为什么会相差这么大呢?这正是神秘的本福特定律在起作用。
本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍,推广来说,越大的数字,以它为首几位的数出现的机率就越低;精确地数学表述为:在b进位制中,以数n起头的数出现的机率为logb(n + 1) − logb(n)。
在十进制中,首位数字出现的概率为:
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| p | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
这个定律的发现,据说是因为本福特在翻对数表的时候发现前面几页被翻得很黑很破烂,越往后越颜色越浅。由此他想到会不会是1开头的数字就是比其他数多,他统计了一下发现果然如此。其实这个对数表的事情真假难辨了,就像是牛顿说自己是被苹果砸到了头才发现的万有引力定律一样,只要最后的定律有用就可以了。
首先说明一下本福特定律的适用范围
这个定律是一个非常神奇的定律,它的适用范围异常的广泛,几乎所有日常生活中没有人为规则的统计数据都满足这个定律。比如说世界各国人口数量、各国国土面积、账本、物理化学常数、数学物理课本后面的答案、放射性半衰期等等数据居然都符合本福特定律。值得一提的是,科学家还发现,统计物理的三个重要分布,Boltzmann-Gibbs分布,Bose-Einstein分布,Fermi-Dirac分布,也基本上满足Benford定律!(来源:李淼的 博客 )
其次这个定律毕竟还是有适用范围的
第一,这些数据必须跨度足够大,必须横跨好几个数量级才能产生这个结果。
第二,有人为规则的数据就不满足次定律,比如说手机号码、身份证号、发票编号等数据,明显不满足这种对数分布律。也就是说,本福特定律正是没有任何限制才显露出来的定律,越是对数据的产生有人为限制,越是不满足该定律。第三,数据不能经过人为修饰,随便人为修改的数据一般就不满足本福特定律了,比如当年著名的安然公司造假案,他们的账本就没有满足本福特定律,因此这个神秘的定律甚至可以用来判别是否财务造假。
那么到底该如何理解这个神秘的定律呢?为何自然产生的数据会满足这么奇特的一个定律,而不是均匀分布呢?
本福特定律产生的根源,就在于指数增长。这幅图可以直观的显示,如果一个变量随时间成指数增长的话,那么这个变量开头的数字随着时间的变化就应该是如下图:(横轴代表时间,纵轴代表那个变量)
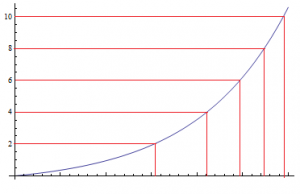
显然,在某时刻你得到它以1开头的概率要大于9开头。而这是只取一个值的情况,如果是取大量的数据的话,在某时刻你观察到他以1开头的数据数量就大于以9开头的数量了。而指数增长的形式在自然界是十分普遍的,只要一个变量的增长率和他的大小成正比,结果就会是指数增长。比如说人类科技发展的速度大致和已有的科技成果成正比,所以人类的科技发展就是个指数增长;人口增长率会和已存在人口数成正比,因此没有资源限制的人口增长也是指数增长。指数增长是自然中极为普遍的一种变化规律,而这种变化规律可以直接导致本福特定律。
另外一种直观的解释(来自维基百科)是这样的
从数数目来说,顺序从1开始数,1,2,3,…,9,从这点终结的话,所有数起首的机会似乎相同,但9之后的两位数10至19,以1起首的数又大大抛离了其他数了。而下一堆9起首的数出现之前,必然会经过一堆以2,3,4,…,8起首的数。若果这样数法有个终结点,以1起首的数的出现率一般都比9大。
就以一个城市的所有门牌号为例,有的街道门牌号可能在100多就结束了,有的在500多结束,有的在900多结束。注意到500多结束那条街一定包含了1、10+和100~199这些1开头的门牌号,而不包含9开头的百位数,只包含9及90+的以9开头的数,这样一来明显以1打头的就多于9打头的了。然后对整个城市的所有街道做一个综合,最终就满足本福特定律了。
以上只是直观的理解,如果想深究它的根本原理,可以参见它的证明
Hill, T. P. “A Statistical Derivation of the Significant-Digit Law.” Stat. Sci. 10, 354-363, 1996.。
另外,值得一提的是,本福特定律满足尺度不不变性,即如果我们换一套单位制,本福特定律仍然成立。其实,这也可以作为大自然产生的统计数据满足该定律的一个解释:如果我们把原来的单位是米的统计数据换一个单位,例如换成英尺或者公尺,那么统计数据的分布应当不变。而唯一满足这种尺度不变性的分布,应当是某种对数分布,也就是本文的主角本福特定律。
