在一个周五晚上,甲和朋友乙决定去夜店High一把。但是他们兴奋过头,忘记了约定的具体时间,只记得是在十二点到一点之间。假设他们随机地选择到达夜店的时间,并且都会在店门口等另一个人十分钟(如果在此期间对方并未出现,他就会离开)。那么,他们当晚能见面的概率是多大呢?
碰面概率是可以算出来的
让我们看看其中一个人甲是怎么想的。站在甲的角度来说,乙可能会在任意一个时间点出现,因此我们可以通过划分时间段的方法,计算碰面的概率。不妨将这一个小时分成三段时间: 00:00 - 00:10, 00:10 - 00:50,00:50 - 01:00。
在第一个时间段内,朋友到达夜店时间是随机的,平均起来就是00:05,所以只要甲在 00 : 00 – 00 : 15 这15分钟内出现都能和乙碰面,因此碰面的概率是 15/60 = 1/4。
类似的,如果乙在第三个时间段内到达,其平均到达时间就是00:55,那么只要甲在 00 : 45 – 01 : 00 这15分钟内出现都能和他碰面,因此碰面的概率也是1/4。
最后我们来考虑中间那一大段,当朋友在这段时间内到达,他的平均到达时间是00 : 30,甲只要在 00 : 20 – 00 : 40 这20分钟内出现都见到他,因此碰面的概率是 1/3 。
把这三种情况综合起来,第一个和第三个时间段长度分别是总时长的 1/6 ,第二个时间段长度是总时长的 2/3 ,我们就可以得到最终碰面的概率是:
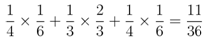
上面这种方法是条件概率方法,很经典,但是过程却稍显繁冗,有没有更好的方法?
更简单的算碰面概率方法
答案是有的,而且这个简单的方法甚至不需要语言。
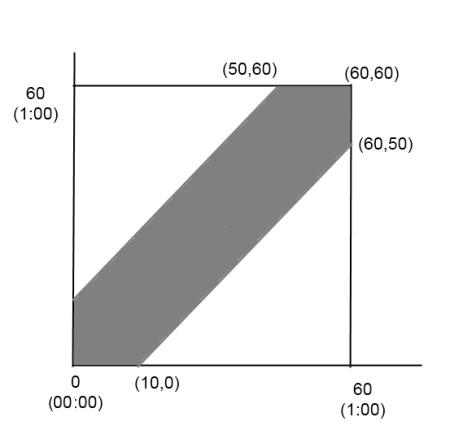
从上图中,你能一眼看出结果么?
如果把甲的到达的时间记在 x 轴上,把乙的到达时间记在 y 轴上,那么他们到达的时间便可以用坐标系中的点 ( x , y ) 来表示,根据设定可知这个点一定会落在图中的正方形区域中。而如果二人想见面,那么他们先后到达的时间间隔一定要小于十分钟,即 | x – y | ≤ 10。
解这个不等式,可得 x – 10 ≤ y ≤ x + 10 。将这两条支线在坐标系中画出来,就能发现它们围成的区域正好是上图的阴影部分。
换言之,如果两人要碰面,对应的到达的时间点 (x,y) 就必须要落在阴影部分内。所以阴影部分的面积与大正方形面积之比就是所要求的概率,据此我们就能很轻松地计算出答案:11/36。
死理性派100%碰面法
当然,上述的分析是在两人到达时间是随机的这个条件下作出的。其实,这个问题真正有趣的地方在于,如果两个人都是死理性派,那他们就是忘了约定时间,一样可以同时到达,保证100%的概率碰面!
第一眼看过去,很容易得出这样的结论:你不会选择离00:00或者01:00太近的时间。如果你出现在00:00,那么你的朋友只能在你之后的10分钟内出现才行。
这很好理解,如果甲在00:00出现,就意味着他的朋友必须在接下来的10分钟内到达。相比之下,显然00:01是一个更好的选择——因为这样的话,乙到达的时间就可以在[ 00 : 00 , 00 : 11 ] 这11分钟内选择。 按照这个逻辑,00:02又比00:01出现更加合适……这样的择优选择可以一直类推到00:10这个时刻。同样的,再考虑时间轴的另一端,我们也可以运用如上的择优法则选择出 00 : 50 这个时刻。这样一来,甲就将自己的出现时间从 [ 00 : 00 , 01 : 00 ] 减小到 [ 00 : 10 , 00 : 50 ] 。因为乙也是死理性派,所以他也一定是这样想的(人以群分嘛)。
于是对于他们两个来说,到达的时间区间变短了,而等待时间不变(依然是10分钟),因此碰面的概率一定会有所提高。事实上,根据之前的方法,如果在这个区间两人随机到达,那么碰面的概率便会增加到7/16。
但是推理就到这一步而已吗?不!人们在选择策略时的逻辑推理过程是这样的:
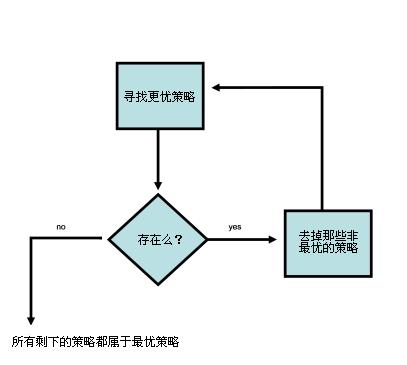
所以只去掉一次非优策略后,甲、乙不会停下思考的步伐,他们只有在确定已经筛选不出更优的策略时才会收手。
前面说过,两人通过各自的推理,确定出了一个新的到达时间区间 [ 00 : 10 , 00 : 50 ] ,但这不会是思考的终点。在新的区间里,再次应用之前的逻辑推理,我们便会发现选择在 00 : 10 出现也是不明智的了,因为两人肯定不会在这个时间点之前出现,于是这样选择就等于只留给对方10分钟,因此 00 : 11 更好——相似的逻辑再次出现。与上一轮思考十分相似,这个区间会被缩减至[00:20,00:40]。
写到这里,想必大家都明白了。没错,这个区间仍然有继续缩减的余地:只要这是个区间(而不是一个时间点),就有继续缩减的余地。按照上面的想法,甲、乙最终都会将到达的时间锁定在 00 : 30 上。所以如果忘记约定时间,两个人就会毫不犹豫地在00:30准时出现,成功碰头。
更一般的,如果等待时间不是10分钟,到达的时间区间也可随意设置,根据上面的分析,两个人仍然会选择在这个区间的中点到达。
实际上,这是一个关于时间的博弈,而 00 : 30 就是纳什均衡点:如果都选择在这个时间点出现,那等待时间将缩减为0,见面机会是100%。所以,如果你的那一位也是一个死理性派,那制造一次浪漫的100%偶遇吧。
本文编译自 mind your decision,原文点 这里 。
