“拒人问题”的数学模型

为了便于我们分析，让我们把生活中各种复杂纠纷的恋爱故事抽象成一个简单的数学过程。假设根据过去的经验，MM 可以确定出今后将会遇到的男生个数，比如说 15 个、30 个或者 50 个。不妨把男生的总人数设为 n。这 n 个男生将会以一个随机的顺序排着队依次前来表白。每次被表白后，MM 都只有两种选择：接受这个男生，结束这场“征婚游戏”，和他永远幸福地生活在一起；或者拒绝这个男生，继续考虑下一个表白者。我们不考虑 MM 脚踏两只船的情况，也不考虑和被拒男生破镜重圆的可能。最后，男人有好有坏，我们不妨假设 MM 心里会给男生们的优劣排出个名次来。

聪明的 MM 会想到一个好办法：先和前面几个男生玩玩，试试水深；大致摸清了男生们的底细后，再开始认真考虑，和第一个比之前所有人都要好的男生发展关系。从数学模型上说，就是先拒掉前面 k 个人，不管这些人有多好；然后从第 k+1 个人开始，一旦看到比之前所有人都要好的人，就毫不犹豫地选择他。不难看出，k 的取值很讲究，太小了达不到试的效果，太大了又会导致真正可选的余地不多了。这就变成了一个纯数学问题：在男生总数 n 已知的情况下，当 k 等于何值时，按上述策略选中最佳男生的概率最大？

如何求出最优的 k 值？

对于某个固定的 k，如果最适合的人出现在了第 i 个位置（k 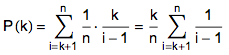< i ≤ n），要想让他有幸正好被 MM 选中，就必须得满足前 i-1 个人中的最好的人在前 k 个人里，这有 k/(i-1) 的可能。考虑所有可能的 i，我们便得到了试探前 k 个男生之后能选中最佳男生的总概率 P(k)：

用 x 来表示 k/n 的值，并且假设 n 充分大，则上述公式可以写成：

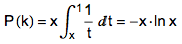
对 -x · ln x 求导，并令这个导数为 0，可以解出 x 的最优值，它就是欧拉研究的神秘常数的倒数—— 1/e ！

也就是说，如果你预计求爱者有 n 个人，你应该先拒绝掉前 n/e 个人，静候下一个比这些人都好的人。假设你一共会遇到大概 30 个求爱者，就应该拒绝掉前 30/e ≈ 30/2.718 ≈ 11 个求爱者，然后从第 12 个求爱者开始，一旦发现比前面 11 个求爱者都好的人，就果断接受他。由于 1/e 大约等于 37%，因此这条爱情大法也叫做 37% 法则。

不过，37% 法则有一个小问题：如果最佳人选本来就在这 37% 的人里面，错过这 37% 的人之后，她就再也碰不上更好的了。但在游戏过程中，她并不知道最佳人选已经被拒，因此她会一直痴痴地等待。也就是说，MM 将会有 37% 的概率“失败退场”，或者以被迫选择最后一名求爱者的结局而告终。

37% 法则“实测”！

37% 法则的效果究竟如何呢？我们在计算机上编写程序模拟了当 n = 30 时利用 37% 法则进行选择的过程（如果 MM 始终未接受求爱者，则自动选择最后一名求爱者）。编号越小的男生越次，编号为 30 的男生则表示最佳选择。程序运行 10000 次之后，竟然有大约 4000 次选中最佳男生，可见 37% 法则确实有效啊。

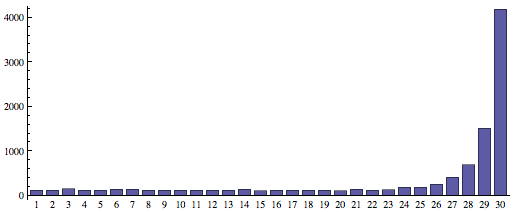
计算机模拟 10000 次后得到的结果

这个问题由数学家 Merrill M. Flood 在 1949 首次提出，这个问题被他取名为“未婚妻问题”。这个问题的精妙之处在于，在微积分界叱咤风云的自然底数 e，竟也出人意料地出现在了这个看似与它毫不相关的问题中。不知道此问题在果壳网上发表后，Geek 男女间会不会多了一种分手的理由：不好意思，你是那 37% 的人⋯⋯