丢番图

“他生命的六分之一是幸福的童年；再活了他的生命的十二分之一，两颊长起了细细的胡子；他结了婚，又度过了一生的七分之一；再过五年，他有了儿子，感到很幸福；可是儿子只活了他全部年龄的一半；儿子死后,他在极度悲痛中度过了四年，也与世长辞了。”

这是一道小学水平的应用题，但如果倒退两千多年，它无疑属于难题。正是这段话，传说被刻在了古希腊数学家丢番图的墓碑上。

丢番图被誉为代数学之父，著有《算术》一书，他对一次方程和二次方程做了深入的研究，其中还包括大量的不定方程。在现代，对于整数系数的不定方程，如果只考虑其整数解，那就把这类方程叫做丢番图方程——因为这基本上正是丢番图当年所研究的内容。古希腊数学家们崇尚几何，认为所有的代数问题只有在一个几何背景下才有意义。丢番图将代数解放了出来，使之成为独立的学科，而且引入了未知数的概念——他的墓志铭就是一道经典的解方程的题目。而那段话既是丢番图一生仅有的传记，也是对他一生成就的最高概括和褒奖。

丢番图的工作在后人的努力下，得到了极大的扩充和发展。 20 世纪最牛数学家希尔伯特在 1900 年数学家大会上提出了 23 个著名的问题，其中的第十个就与丢番图方程密切相关。

一个方程最基本的特征之一就是它是否有解，丢番图方程也不例外。例如经典的勾股定理对应的丢番图方程：

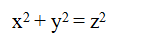
就是有整数解的，而且有无穷多组解。而与此很像的是费马大定理方程：

就不存在非平凡的整数解。

两个长得如此之像的丢番图方程结果居然完全不同，历代数学家经过数百年的探索后，最终使用了当年的费马不敢想象的数学工具才艰难地得以证明。在人们解决费马大定理之前，希尔伯特提出了他的第十个问题：是否存在一种只有有限步骤的方法，使得我们能够判断任意一个丢番图方程的可解性？

如果存在这样的办法，那对费马大定理的证明就变成了很平凡的步骤，许许多多的数学问题也能巧妙地转化成一个丢番图方程进行解答了。因此，这个问题就相当于是在寻找数学中的一个“通法”，如果能找到，那么全世界所有数学家都会去研究丢番图方程和自己的研究领域的关系了，世界将是多么的美好。然而，并不完美的世界还是给了我们一个不完美的答案。 1970 年，前苏联数学家 马季亚谢维奇 给出了否定的答案，也就是说，不能在有限步内判断任意丢番图方程是否有解，更进一步地，我们甚至可以构造出一个无法证明其是否可解的丢番图方程！实际上，数学家们在 1900 年对这个问题没有任何的概念，直到在图灵提出了他著名的 停机问题 后才对此有了初步的认识，在此之后，数理逻辑和计算机得到大力发展，最终解决了许多重大难题，丢番图方程的不可解性就是其中之一。丢番图先生当年做这些研究，可能想不到他手下的这些式子会延伸出如此多的奇妙变化吧。

阿基米德

这位数学全才生前的最后一句话响彻寰宇：“不要踩坏我的圆！”他的墓碑上面也正是遵照他早已明确的意思，刻上了一幅与圆有关的图像：圆柱体与其内接球的体积比和表面积比都是 3 : 2 ——显然，阿基米德对这个结果很满意。

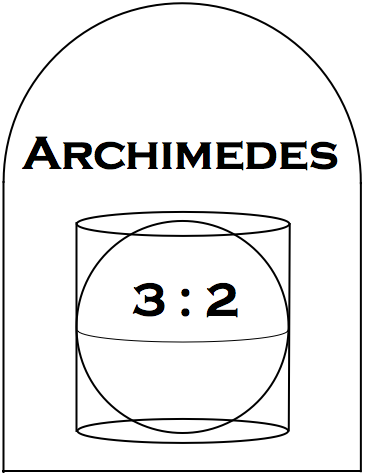
阿基米德完善并发展了前人提出的“穷竭法”，穷竭法由古希腊的安提芬( Antiphon )最早提出，他在研究“化圆为方”问题时，提出了使用圆内接正多边形面积“穷竭”圆面积的思想。后来，古希腊数学家欧多克斯( Eudoxus of Cnidus )做了改进，将其定义为：在一个量中减去比其一半还大的量，不断重复这个过程，可以使剩下的量变得任意小。阿基米德进一步改进这种方法后，将其应用到对曲线、曲面以及不规则体的体积的研究和讨论上，为现代积分学打开了一道隐隐的门。

他的著作《论球和圆柱》全篇以穷竭法为基础，证明了许多的相关定理。其中命题 34 的陈述是：任一球的体积等于一圆锥体积的4倍，该圆锥以球的大圆为底，高为球的半径。实际上，他的墓志铭就是这个命题的推论。

这个精力旺盛而长寿的天才还通过使用圆外接正多边形和圆内接正多边形逼近圆周率的真实值，他最终使用到了九十六边形（因为 96 = 2 ⁵ * 3 ，稍后我们会在后面发现这个多边形正巧是可以通过尺规作图做出来的），得到π的真实值在 3.14163 和 3.14286 之间。

高斯

高斯被称作“数学王子”，在民间也流传着许多与他声誉相符的故事。但是，他的墓碑上刻的并不是地球人都知道的等差数列求和公式，也不是他独立给出四种证明的代数基本定理，而是一个在尺规作图领域中被人津津乐道的漂亮结果：尺规作出正十七边形。

作图的方法陈述起来过于繁琐，这里我们用一张动态图，一步一步地展示出作图的方法：

有趣的是，高斯不仅给出了做法，还证明了能够通过尺规作图做出的正多边形需要满足的条件是边数目必须是 2 的非负整数次方和不同的费马素数的积。这个费马素数是什么呢？

费马是一个拥有着大师水准的业余数学家，提出过许多的猜想和定理，很多都在他死后被证明是正确的，而“费马素数”却是他为数不多跌了跟头的地方。费马在 1640 年提出，所有的形如

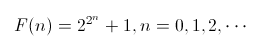
的数字都是素数。这个数列的前 5 个数的值分别是 3, 5, 17, 257 和 65537 ——确实都是素数，看起来费马先生要赢了。但欧拉却指出 F( 5 ) = 641×6700417 不是一个素数，后来随着计算机技术的发展，大家从 F( 5 ) 开始就再也没有找到素数了。但谁也想不到的是，费马的这个失误意外地和尺规作图联系到了一起。

根据高斯的结论，正多边形边数只有在 K = 2 ⁿ × ( 2 ^₂m + 1 ) ，其中 n，m= 0，1，2，… 时才能通过尺规画出来。将正 n 边形的每一条边对应的圆弧二等分，我们可以轻易地做出正 2n 边形。因此，“正 F( m ) 边形”可以说是产生所有这些可被作图正多边形的“因子”。这是一个延绵了两千多年的尺规作图难题，较其同类们十分幸运地在高斯手中得到了一个肯定的回答。在高斯之后，也有人陆续给出了正 257 边形和正 65537 边形的尺规作图过程。其中正 65537 边形的作图过程十分繁琐，单单做图方法的计算手稿就有 200 页，完整的过程更是装满了一个皮箱，现在被收藏于高斯的母校哥廷根大学。在 这里 我们可以围观维基百科上的正 65537 边形（ 需要SVG Viewer等软件 ）。

鲁道夫

当你看到这个名字的时候，第一反应是不是这样的：鲁道夫？我怎么不知道还有叫这个名字的数学家？

确实，这位数学家不是最出名的，甚至可能是最不出名的（之一），但是他的墓碑一定是最霸气的。他的墓碑完整地概括了其一生的经历：

3.14159265358979323846264338327950288..

是的，他墓碑上的主要内容就是一个 π 的精确到小数点后 35 位近似值——实际上，他这辈子的大部分时间都在算这个数字！

这位德国数学家的全名是鲁道夫·范·科伊伦（Ludolph van Ceulen），他在 1600 年成为荷兰莱顿大学的第一位数学教授，但是把主要精力全都放在了求解圆周率的更精确的值上。在那个计算基本靠手的年代，他选择了前文提到的简单而繁琐的阿基米德式方法对圆周率进行逼近，最后得到墓碑上的结果的时候，使用的多边形已达到了惊人的 262 条边！相比之下，阿基米德倒稍显“平淡无奇”。由于使用了阿基米德的夹逼法，所以墓碑上其实给出了圆周率的上界和下界。

看来把一件事情做到极致，那就是伟大。鲁道夫的这种精神无疑让很多人佩服，以至于圆周率在德国被称为鲁道夫数。到今天，人们已经把鲁道夫先生的工作向前推进了很多很多，计算圆周率也已经成为了考察计算机运算能力的一个方式。作为在这个道路上跨出坚实一步的人，鲁道夫先生一定也含笑九泉的吧。

你想在你的墓碑上刻点什么呢？

本文部分内容编译自： what do you want on your tombstone