俗话说,狭路相逢勇者胜。不过从死理性派的角度来看,有勇无谋不足夸,智勇双全才是王道。天生胆小没关系,只要你有大智慧,一样能够死磕到最后。让我们一起来看看如何才算谋定而后动,知止而有得。
胆小鬼博弈
假设这样一种情形:两名赛车手各自驾驶汽车沿着一条划定的直线相向而行,相撞前首先转向的一方就是“胆小鬼”,英语中常用 chicken 来形容胆小的人,所以这个假想游戏也被称为 chicken game。虽然听起来有些荒诞,不过在电影和现实中这种情境并不少见,比如《天下无贼》中刘德华与黎叔手下的四眼在火车顶上“比胆”,两人站在疾驰的火车上,迎面而来的是黑洞洞的隧道,先蹲下的那个自然是输了比赛,但坚持到最后却需要极大的胆量,稍有不慎就会“肝脑涂地”。《裸婚时代》中也有类似的情节,主角刘易阳与樊少爷在地下停车场打赌,看谁最后刹车后离躺在地下的姑娘最近。此外,现实中的劳资谈判问题也可以看做是胆小鬼博弈——双方都不妥协必然就会两败俱伤,一方妥协往往意味着重大让步。
在胆小鬼博弈中,我们假定双方可以采取的策略只有 2 种:死磕到底(用Dare或D表示)或者认怂(用Chicken或C表示),双方(甲、乙)采取不同策略的收益可以用下表来表示:
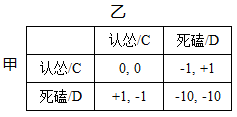
这里数字的绝对值并不十分重要,主要是用来表示双方损失或收益的的相对大小。通常一个结果可以用(D, C)这样的形式来表示,即甲方死磕到底,乙方最终认怂。
认怂固然丢面子,但相比玉石俱焚的结果来说,保命显然更重要。因此对一个足够理性的人来说,应该在他能够控制的最后时刻选择C策略,即果断认怂。而如果甲方相信乙方是一个足够理性的人的话,那他应该能够预料到乙方会在最后时刻放弃,所以甲方的最佳策略是死磕到底(D策略),对应的结果就是(D, C),类似的情况反转过来是(C, D)。当然要是双方都这么想的话,最后的结果很可能是(D, D)。有趣的是,在胆小鬼博弈中当一方的选择受到了限制时,其赢面 可能 会变大。例如在赛车的虚拟游戏中,甲方的方向盘被锁死,不得不选择 D 的话,乙方再傻也会知道识时务者为俊杰,选择 C 的结果 -1要远好于同归于尽的 -10。

图片来源:emirates247.com
通常, (C, D) 和 (D, C) 被称为胆小鬼博弈的纳什均衡点,即在这个状态下,如果一方不改变其策略,不论对方采取什么策略都不会有更大收益。例如对于 (D, C) 而言,甲方心意已决,就算乙方将对策由认怂改为死磕,结果也是两败俱伤而不会收益更高。类似的,如果乙方已经决定认怂,甲方不再死磕也选认怂的话,其收益将从 +1 变为 0。
这两个纳什均衡点被称为“纯策略均衡点”,即双方采取的是一个 C 和 D 之间一个确定策略。而当甲乙至少有一方采取的策略是不确定的时候,我们可以用下图来表示双方的决策:
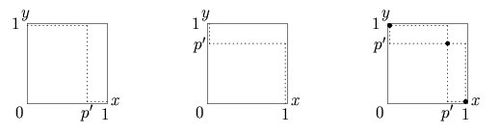
其中 x 表示甲方的策略, y 表示乙方的策略,位于 [0,1] 区间的 p' 表示某方采取 D 策略的概率。左边的图意味着甲方以概率 p' 采取 D 策略,乙方则一定会根甲方 D 到底。中间的图表示相反的情形。右边的图表示甲乙双方是否采取 D 策略都都属于不确定事件,两条虚线的交点就是胆小鬼博弈的第三个纳什均衡点(混合策略均衡点)。假定甲乙双方无差别,也就是说他们都以同样的概率 p' 来决定是否死磕到底(策略D),因此混合策略均衡点总是在对角线上。
现实中的例子:劳资谈判

图片来源:mywelcometothecity.com
一般来说,混合策略的纳什均衡点只是局部最优,换言之,如果双方能够在某种意义上“合作”的话,收益将大于混合策略均衡点的情形。让我们来考虑一个实际中的例子:劳资谈判。这里同样用 C 来表示妥协, D 表示坚持:
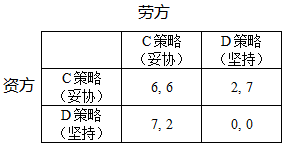
假定劳资双方在充分考虑损失后,都决定以 1/3 的概率选择 D 策略,那他们的期望收益(因为表中的收益是对称的,只需要计算一方的结果即可)就是:
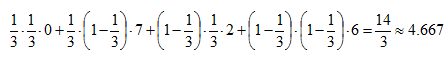
如果现在有一个第三方机构介入(比如某个调解机构),这个机构可能给出的裁决结果是 (C, D)、(D, C) 和 (C, C) 中的一个,三种结果的概率各为 1/3。在该机构裁决后,会分别向劳方和资方通报他们各自应当采取的策略,但不告诉他们对方得到的结果。从收益上讲,尽管不知道对方被告知的策略是什么,劳资双方仍然会倾向于接受该机构的裁决。因为拒绝接受这个调解策略也不可能有更大收益。
比如劳方被告知应当采取 D 策略,那资方一定会被建议采取 C 策略(双输的结果不在可能的裁决范围内),显然这是最有利的结果。如果劳方被告知应当采取 C 策略,可以认为资方被告知选 C 策略和 D 策略的可能性分别是1/2,所以资方期望收益就是:
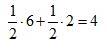
如果劳方对这个裁决结果不满意,强行采取D策略,期望的收益则会变为:
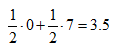
这个收益小于劳方接受裁决结果的期望收益。因为资方和劳方的收益表是对称的,同样的分析也适用于资方。
由此可见,一方不论被建议的策略是 C 还是 D,接受该策略的期望收益都大于采取另一策略的情形。当然在现实中,双方的收益表、损失评估(即采取不同策略的概率)和第三方机构作出不同裁决的可能性都会有所变化,对具体的例子,是否接受裁决结果仍然要计算以后才能知道。
史上玩的最大的胆小鬼博弈:古巴导弹危机

历史上玩的最大的胆小鬼博弈可能就是古巴导弹危机了。 1962年,为报复美国在意大利和土耳其部署的针对苏联的核导弹,苏方在古巴境内秘密部署针对美国的核导弹,但这一举动很快被美国发现。一时间美苏双方针锋相对,互相威胁将冷战升级为热战,在 13 天的危机交涉中,双方军队在加勒比海地区险些擦枪走火。最终双方相互妥协,苏联撤走了部署在古巴的导弹,美国保证不会入侵古巴并承诺稍后撤走部署在土耳其的导弹。
在古巴导弹危机中,美苏双方都在实践美国前国务卿杜勒斯在 1956 年提出的战争边缘理论(Brinkmanship),杜勒斯说,“不怕走到战争边缘,但要学会走到战争边缘,又不卷入战争的必要艺术”。
在博弈论中,有时也用“边缘博弈”来表示一种特殊的胆小鬼博弈:双方在尽量对自己有益的情况下避免双输局面。像劳资谈判这种情况,要是实在达不成共识,大不了一拍两散。但对两个手握核武器的超级大国来说,问题就不这么简单了。
在边缘博弈中,双方往往互相恐吓,恐吓的关键在于让对方相信自己有能力也有决心实现这些恐吓(甚至是让对方相信自己出于某些不可控制的原因必须毫不退让)。假如美国刚发现苏联在古巴部署的导弹就威胁要对苏联本土的全部军事目标实施核打击,那这就是一个不很可信的恐吓,因为苏联会怀疑美国是否有这样的决心在刚有风吹草动时就全面开战。
事实是美国宣布要封锁古巴,这就是个可信的威胁,美国具有这样的能力也很可能有这样的决心。但美国封锁古巴对其影响仍然有限,所以苏方继续在古巴部署导弹并声称封锁不可接受,还声称导弹只是防御性质的。这说明尽管美国的恐吓是可信的,但其程度仍然不能阻吓对方。

美国为了证明自己言出必行,果然开始封锁古巴。并在次日,美国战略空军司令部战备级别提高, B-52 进入 15 分钟起飞状态, 145 枚洲际导弹进入发射准备。肯尼迪向他的国家安全执行委员会表示唯一的解决办法是入侵古巴,苏联此时仍没有任何退让的意思,双方陷入僵局。
另一方面,在美苏秘密接触进行外交努力的同时,似乎双方的军队和古巴方面已经不受控制了。美军进行了一次运载火箭发射试验却没有通知肯尼迪的执行委员会。一架 U-2 侦察机未经授权对苏联远东地区进行了 90 多分钟的越境侦查。一架海军飞机向一艘位于古巴附近的苏联核潜艇投掷了深水炸弹(美当时不知道这艘潜艇携带了核弹头),要知道苏联艇长在出航前收到的命令是开战后可自行决定是否使用核导弹,在核导弹已做好发射准备的情况下,这艘潜艇还是放弃了发射,决定上浮。而美国派往古巴的侦察机也被防空导弹和高射炮击落。
就在所有人都以为第三次世界大战不可避免时,事情峰回路转。肯尼迪决定不进行报复并密电赫鲁晓夫表示同意赫氏的建议,撤回部署在土耳其的导弹并保证不入侵古巴,以此作为苏联撤回古巴导弹的交换条件。古巴导弹危机随即得到解决。
在边缘博弈中,最重要是要让对方相信自己的恐吓绝不是虚张声势,甚至让对方相信自己的决策是身不由己(例如美国军方的某些行动就没有经过肯尼迪的同意)。由于双方都有强烈的愿望避免双输的局面出现,因此最终的结果往往都是双方达成一致,各自妥协。
当然,古巴导弹危机本身牵涉甚广,除美国和苏联之外古巴也扮演了重要角色(例如卡斯特罗曾密电赫鲁晓夫建议苏联先下手),此外美苏国内各方的压力也对各自的决策产生了影响,因此很难以最简单的胆小鬼博弈来分析,有兴趣的读者可以参考 这篇文章 ,作者 Steven Brams 是美国纽约大学政治系的教授,他以对政治学和博弈论的研究而知名。
主要参考资料:
[1] 维基百科: chicken game
