球面上的圆形帝国

首先让我们先考虑简单一点的情形。假设地球是一个标准球体，你的帝国是地球上一个巨大的圆形。如图所示，这个圆将地球表面分为两部分，上面那部分就是你的帝国。假设地球的半径是 R，帝国中心到帝国边界所在平面的距离是h，现在我们来计算帝国的面积。

我们先用若干个与边界圆平行的平面将帝国分割为一个个细窄的环带。每个平面间的距离是 Δh。

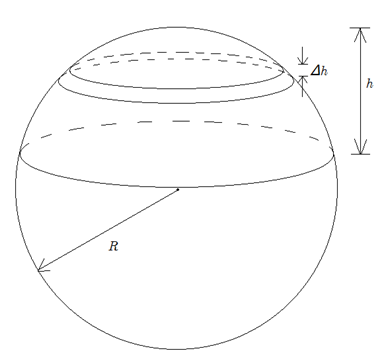
考虑其中一个环带，当 Δh 足够小时，环带的上边缘和下边缘的长度相差就很小。假设环带上一点到球心连线与帝国中心到球心连线的夹角为 θ，那么这个环带的边缘的长度近似等于 2πRsinθ。根据半径与球面的垂直关系，可以得出这个环带上下边缘之间的一条最短的线段与用于切割的平面的夹角也是 θ，所以这个环带的宽度是 Δh/sinθ。然后就可以得出这个环带的面积是 2πR sinθ×Δh/sinθ = 2πRΔh。从这里可以看出，所有的环带的面积都相等，都是 2πRΔh。

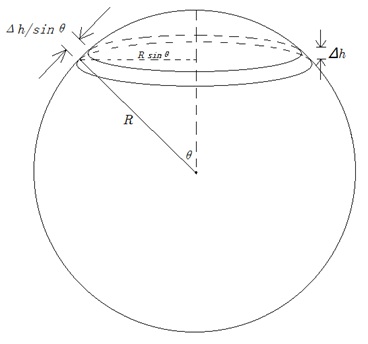
如果我们将这些环带的面积加起来，就能得到帝国的面积是 2πRh。

如果把帝国中心到帝国边界的直线距离记为 L，如图，由相似三角形的关系，可以推出 2Rh = L²。所以帝国的面积可以写为πL²，它与平面上一个半径为 L 的圆的面积相等。

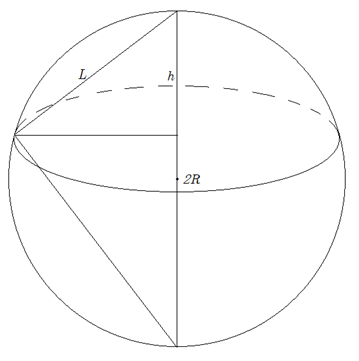
如果你征服了全球，就会有 L = 2R，根据上面的公式，你的帝国的面积是 4πR²。这正是整个地球的表面积。

实际上，上面所写的球表面积公式以及球面上的圆面积公式最早是由古希腊的阿基米德得出的。他在《论球和圆柱》中用穷竭法证明了这个定理。穷竭法由古希腊的安提芬( Antiphon )最早提出，他在研究“化圆为方”问题时，提出了使用圆内接正多边形面积“穷竭”圆面积的思想。后来，古希腊数学家欧多克斯( Eudoxus of Cnidus )做了改进，将其定义为：在一个量中减去比其一半还大的量，不断重复这个过程，可以使剩下的量变得任意小。阿基米德进一步改进后，将其应用到对曲线、曲面以及不规则体的体积的研究和讨论上，为现代积分学打开了一道隐隐的门。

球面上的三角形帝国

算出了圆形帝国的面积，我们再来考虑复杂一些的情况，假如你的帝国是地球上的一个多边形。

先定义什么是球面上的多边形。在球面上，两点间最短的距离是大圆的弧线段的长度。所谓球面上的大圆，指的是圆心与球面的球心重合的圆（例如地球的经线都是大圆，而纬线只有赤道是大圆）。这种连接曲面上两点的最短弧线称为测地线，顾名思义，它是由古代的数学家们测量两地距离时发现的。而一个球面 n 边形，就是由 n 条测地线段首尾相连所组成的闭合图形。与平面的情形类似，每条测地线段称为多边形的边，两条测地线段的交点称为顶点。顶点处两条测地线的切线的夹角就是多边形的内角。

不妨先算一个三角形帝国的面积。设地球的半径为 R， △ABC 是其上一个球面三角形。我们分别以 α，β，γ表示三个顶点的内角，仍然用 △ABC 表示它的面积。延长三角形的三条边，将其延长为完整的大圆。球面上的两个大圆会有两个交点，这两个交点是球面的一条直径的端点，这样的两个点称为对径点。记A，B，C的对径点分別是A'，B'，C'。

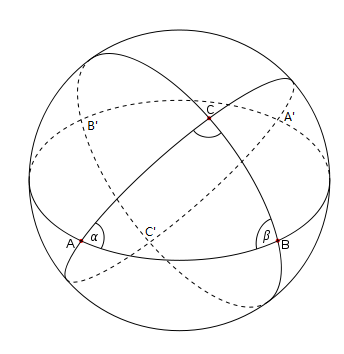
我们考虑半圆弧 ABA' 和半圆弧 ACA' 所围成的区域。由于球面关于直径 AA' 是旋转对称的，所以我们可以推出这块区域与整个球面的面积之比为 α/2π。前面我们已经得出球面的面积公式是 4πR²。所以这块区域的面积是 2αR²，即

△ABC + △A' BC = 2αR²

按照同样的方法，我们还可以得出：

△ABC + △AB'C = 2βR²

△ABC + △ABC' = 2γR²

因为 △ABC' 和 △A'B'C 关于球心对称，所以它们的面积相等：

△ABC' = △A' B' C

又由于上述三角形的其中四个可以拼成半个球面：

△ABC + △A'BC + △AB'C + △A'B'C = 2πR²

所以根据以上 5 个方程，可以解出：

△ABC = (α+β+γ－π)R²

这就是球面三角形面积公式。它最早是由英国数学家托马斯•哈里奥特发现的，但被称为笛沙格定理，因为法国数学家吉拉德•笛沙格最早地将这个定理发表了。

高斯眼中的球面三角形

一个很有意思的地方是，球面三角形的内角和大于π。也就是说球面几何其实是一种 非欧几何 。

当年，高斯在主导汉诺威公国的大地测量工作时，他通过测量三座山峰Brocken、Inselsberg、Hohehagen所构成的三角形的内角和，以此验证非欧几何。最终测出这个三角形的内角和为 180°0′14.85″。不过高斯认为这什么也证明不了，因为测量误差可能就远大于 14.85″。三座山峰构成的三角形太小了，只有在更大的三角形中才能看出其内角和与π的显著差距。此时高斯已经认识到了非欧几何的深远意义：非欧几何在逻辑上是相容的，它可以来描述物质空间，和欧氏几何一样地正确，欧氏几何并不是物质空间所必然有的几何。

仿照平面几何中的思路，我们可以把球面上的多边形分割成若干个三角形。如此就能算出球面上多边形的面积。

一个球面 n 边形可以分割为 n－2 个球面三角形，对每个三角形应用上面的公式，然后把这些等式加起来，我们就得到球面上 n 边形的面积公式：

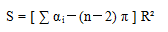
其中 α _i 是 n 边形的 n 个内角。

如果我们用外角（外角是内角的补角）来表示这个公式，它可以写得更简洁：

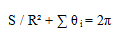
其中 θ _i 是 n 边形的 n 个外角， θ _i = π－ α _i 。

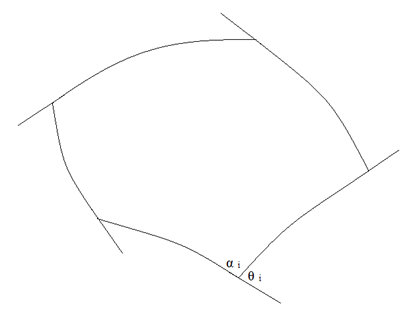
按照这个公式，你只要沿着帝国的边界走一圈，回到原来的位置、原来的方向，那么你转过的角度与2π的差值就代表了帝国领土的大小。

最后再来介绍一下更一般的情形。假如有一个光滑的曲面，在这个曲面上有一个由测地线组成的三角形，那么对这个曲面三角形，有

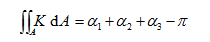
其中K是曲面的高斯曲率，dA 表示对面积的积分， α ₁ 、 α ₂ 、 α ₃ 是三角形的三个内角。

一个半径为R的球面的高斯曲率等于 1/R²，于是我们可以看到，球面三角形面积公式是上面这个公式的特例。这个公式是高斯在《关于曲面的一般研究》中证明的。

高斯的这篇文章提出了一个全新的概念，即一张曲面本身就可以看成是一个空间。随后这个概念得以推广，从而为非欧几何学开辟了一片新的天地。