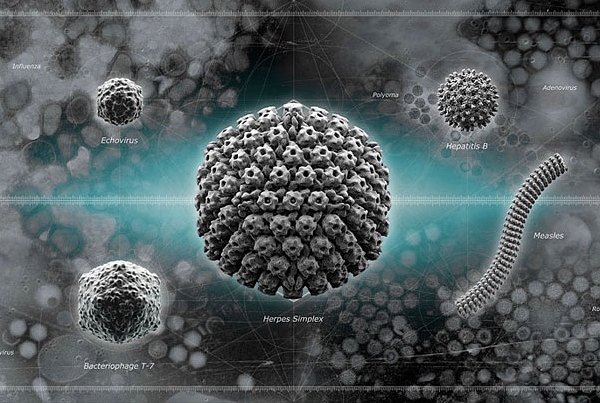
一些拥有对称性结构的常见病毒,体积按比例绘制(图片:Molecluar Machines)
(文 / 伊恩 · 斯图尔特)病毒——人类和动植物大部分疾病的起源——的结构,也可以用数学来解释。病毒比多数的生物分子大,却是细菌的 100 万分之一。病毒的数量庞大(是人类的 10250 倍),种类繁多(已知的病毒种类已经超过 5000 种,总数可能超过百万)。病毒的遗传物质包裹在蛋白质里面,每种病毒都有一种特定的结构,大部分是十二面体的或者螺旋形的:就像足球形状或者螺旋楼梯。
了解病毒结构能够为疾病治疗提供新方法,这就要用到主要的数学工具之一——几何,但也有一个难点:需要在多维空间中计算。经典的欧几里得几何学,描述的是二维(平面)和三维(空间)。分析病毒的形状需要用到一个我们不熟悉的概念: 六维空间几何学 。不是指病毒来自 “六维空间” ,而是六维数学能更好地了解三维空间中的病毒,因为病毒复杂的三维形状,就可以成为六维空间中的缩影,或者其中的一片,并且变得更简单易懂。
要知道什么是六维空间几何学,还得先从三维空间说起。
经典欧式(欧几里得)几何学确定了 5 个正多面体:正方体、正四面体、正八面体、正十二面体和正二十面体。正方体的面是四边形,十二面体的面是五边形,其他 3 个图形的面是三角形。
欧式正二十面体很漂亮,却在 2000 多年的时间里缺乏实际应用。其实,二十面体正好是病毒的最佳形状。为什么会这样呢?一部分原因来自能量。病毒的外衣一般都是由单个蛋白质分子的多次复制组合而成,并且每个病毒的外衣都不一样。当这些分子尽可能聚合成接近球体时,将具有一些低能量。病毒的糖衣蛋白不能形成精确的球形(就像把 100 个网球放在一起,也不能使它变成一个光滑的球体一样),但是病毒在努力接近球形。在欧式正多面体中,正二十面体是最接近球形的,只要将角切掉,它就是一个球了,因此国际正规赛事中用的足球,大部分是正二十面体组成的。
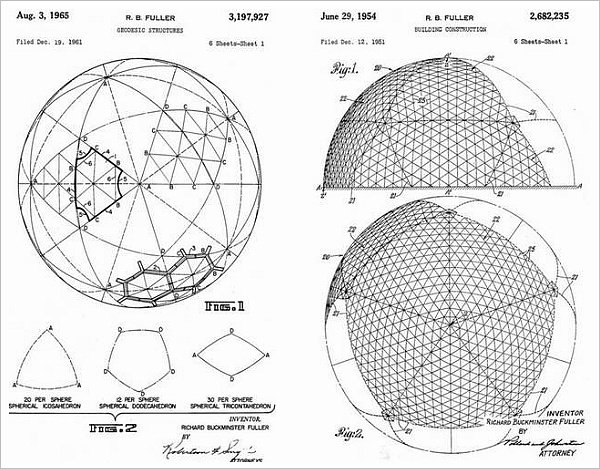
美国建筑家巴克明斯特·富勒(Buckminster Fuller)的设计专利图纸。从左边的设计图上,我们可以想见,正二十面体(面是三角形)和正十二面体(面是五边形),是如何构成球体的。右边的设计图,是不是让你想起了足球的形状呢?(图片:inventors.about.com)
病毒的二十面体糖衣蛋白是由 20 个三角形组成,每个三角形都是蛋白质单元的排列,就像最初的斯洛克台球一样。在 1962 年,生物学家唐纳德·卡斯帕(Donald Caspar)和阿隆·卡兰格(Aaron Klug)意识到,他们在建筑师巴克明斯特·富勒(Buckminster Fuller)的建筑作品中,看到过这样的排列。
富勒因 “网格状球顶” 而著名,这种球顶由大量的三角面板组合在一起,结构近似球形。卡斯帕和兰格发现,大多数的病毒也有类似富勒球顶的几何结构,形成 “伪二十面体” 。称为 “伪”,是因为这 20 个三角形的每个面,都被细分为了更小的三角形。
几何学能够预言形成病毒表面蛋白质单元的个数的一些特殊情况,比如 32,42,72,92,162,252 和 362。这与病毒的真实情况非常吻合,比如传染性犬肝炎病毒的蛋白质结构有 362 个单元、人瘤病毒蛋白有 72 个单元。这两种病毒的结构都类似网格球顶。然而,在卡斯帕-克鲁格理论(Caspar-Klug)中也有例外的情况,比如导致类人猿或者人类患肿瘤的猿猴空泡病毒。

美国建筑家巴克明斯特·富勒及其标志性作品,网格状球顶(图片:CSU ARCHV/EVERETT/REX FEATURES)
10 年前,德国数学家雷登·特瓦克(Reidun Twarock)提出建议,发展更一般的、基于正二十面体对称性的病毒几何学理论。与欧式几何不同的是,她研究的不是三维空间,而是六维空间。这并不像听起来的那么复杂,因为这里的 “维度” 广义上所指的是 “方程中的变量” 。试想一下太阳系:如果你想指出地球的位置,你需要知道它处在三维空间的坐标(这就需要 3 个变量),还需要知道它在太空中的移动速度(又需要 3 个变量),总共需要 6 个变量。如果你要指出太阳的位置,则又需要另外 6 个变量。对于月亮也是如此。
于此而言,数学知识表明,我们在研究运动时需要采用十八维空间。在任意条件下,物体的实际构型是三维的,三维空间是十八维空间的一个“缩影”。我们通常将三维问题转化为二维问题考虑,比如把三维的树画到二维的纸上。同理可将六维或者十八维变量,转化到三维空间中,只是多了几个变量而已。
特瓦克就是运用这种思想,把病毒的 3D 结构想象成了更高维度结构的简单缩影。举个例子,你用大量的立方体堆成一个 3D 的棋盘,用特定的方式切开它,就能得到一个美丽的瓷砖图案。仰视这个切面,可以发现都是三角形和六角形。原来的堆积物只有一个形状,就是立方体结构,但是在切面处却出现了两个不同的形状。换言之,就像分别从前面、侧面观察一只猫。在二维空间中,观察到的形状是截然不同的。但是在三维空间中观察真实的猫,才发现原来是不同部位的形状在起着作用。
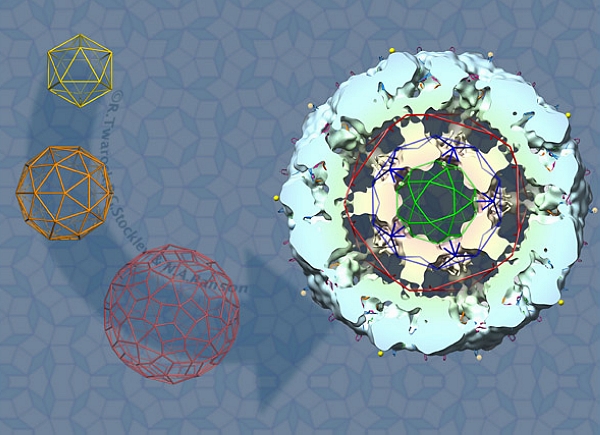
病毒结构模型的演化,从沃森-克里克,到卡斯帕-克鲁格理论,最终到特瓦克模型(图片:plus.maths.org)
特瓦克用了相似的巧妙方法,来研究二十面体病毒的蛋白质单元。科学地讲,二十面体是高度对称的:有 120 种方法去旋转或者反射使其保持不变。如果这些单元的排列来自于一个更高维度空间的模型,那么这个模型就相应地有 120 个相同对称面。
关于处理这种问题的方法,存在一个成熟的数学分支,称为群论。它列出了六维空间中特殊模型清单。群论发展了卡斯帕-克鲁格理论,它可以解释猿猴空泡病毒和其他病毒的特殊结构,且具有潜在应用:阻止病毒扩散的方法之一,便是干扰病毒的形成——了解一个完整病毒的几何结构,可以揭示出该病毒在形成过程中至关重要的薄弱环节。
此外,二十面体病毒有时候会改变形状,成为不具有传染性的立方体。所以把病毒的二十面体形状变成立方体形状,或许就可以干扰病毒的复制,进而预防疾病。如果科学家可以重编病毒使蛋白单元管状排列,或许会消灭病毒的危害性。
(接下来在生物数学系列的第三篇中,我们将介绍浮游生物悖论,还有想象中的那头球形奶牛~)
生物数学系列
| 编译说明: |
|---|
| 文章题图: | pretty-pix.blogspot.com |
|---|---|
| 内文图片: |
[1] Molecluar Machines,via vir.gla.ac.uk;
[2] inventors.about.com;
[3] CSU ARCHV/EVERETT/REX FEATURES,via m.sciencegallery.com;
[4] plus.maths.org.
|
